Hoạt động 1
a) Cho hàm số \(f\left( x \right) = {x^2}\)
Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { - x} \right)\) và \(f\left( x \right)\)
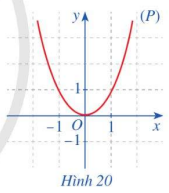
Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?
b) Cho hàm số \(g\left( x \right) = x\)
Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { - x} \right)\) và \(g\left( x \right)\)
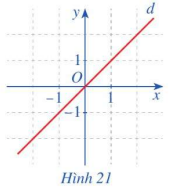
Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.

Dựa vào kiến thức về hàm số để xác định

a)
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d
Luyện tập - VD 1
a) Chứng tỏ rằng hàm số \(g(x) = {x^3}\)là hàm số lẻ.
b) Cho ví dụ về hàm số không là hàm số chẵn cũng không là hàm số lẻ.

Sử dụng định nghĩa hàm số chẵn, hàm số lẻ.


Advertisements (Quảng cáo)
a)
Hàm số \(g(x) = {x^3}\)
+) Có tập xác định D = R;
+) Với mọi \(x \in R\)thì \( - x \in R\)
Ta có \(g( - x) = {\left( { - x} \right)^3} = - {x^3} = - g(x)\)
Vậy \(g(x) = {x^3}\)là hàm số lẻ.
b)
Ví dụ về hàm số không là hàm số chẵn không là hàm số lẻ là
\(f(x) = {x^3} + {x^2}\)
Hoạt động 2
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.
a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?
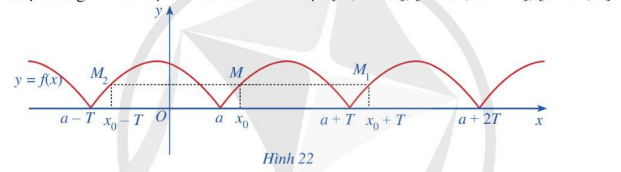
b) Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)

Dựa vào cách nhìn đồ thị để trả lời câu hỏi

a) Đồ thị hàm số trên mỗi đoạn là như nhau
b) \(f\left( {{x_0} + T} \right) = f\left( {{x_0} - T} \right) = f\left( {{x_0}} \right)\)
Luyện tập - VD 2
Cho ví dụ về hàm số tuần hoàn

Sử dụng định nghĩa về hàm số tuần hoàn.

Ví dụ về hàm số tuần hoàn là : \(g(x) = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,,x \in Q\\1\,\,\,\,\,\,\,\,,x \in R\end{array} \right.\)
