Hoạt động 5
Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1
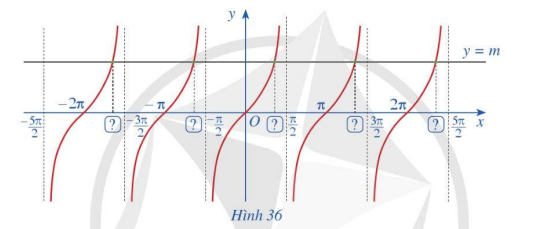
a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = 1

Dựa vào phương trình lượng giác của sinx và cosx để làm bài

a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
Advertisements (Quảng cáo)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
Luyện tập - VD 7
a) Giải phương trình \(\tan x = 1\)
b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\)

Sử dụng công thức tổng quát để giải phương trình tan

a) \(\tan x = 1 \Leftrightarrow \tan x = \tan \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
b) \(\tan x = \tan {67^ \circ } \Leftrightarrow x = {67^ \circ } + k{.180^ \circ }\)
