
Cho tứ diện đều \(ABCD\). Vẽ hình bình hành \(BCED\).
a) Tìm góc giữa đường thẳng \(AB\) và \(\left( {BCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,CD,B} \right];\left[ {A,CD,E} \right]\).

‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a’\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a’} \right)\).

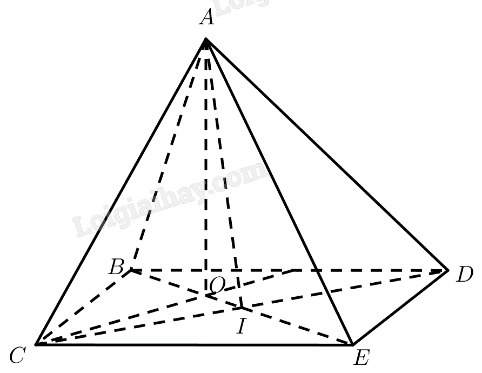
a) Giả sử tứ diện đều có tất cả các cạnh bằng \(a\).
Gọi \(I\) là trung điểm của \(CD\), \(O\) là tâm của \(\Delta BC{\rm{D}}\)
\( \Rightarrow AO \bot \left( {BC{\rm{D}}} \right)\)
\( \Rightarrow \left( {AB,\left( {BC{\rm{D}}} \right)} \right) = \left( {AB,OB} \right) = \widehat {ABO}\)
Advertisements (Quảng cáo)
\(BI\) là trung tuyến của tam giác đều \(BC{\rm{D}}\)
\( \Rightarrow BI = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow BO = \frac{2}{3}BI = \frac{{a\sqrt 3 }}{3}\)
\(\cos \widehat {ABO} = \frac{{BO}}{{AB}} = \frac{{\sqrt 3 }}{3} \Rightarrow \widehat {ABO} \approx 54,{7^ \circ }\)
Vậy \(\left( {AB,\left( {BC{\rm{D}}} \right)} \right) \approx 54,{7^ \circ }\)
b) \(\Delta AC{\rm{D}}\) đều \( \Rightarrow AI \bot C{\rm{D}}\)
\(\Delta BC{\rm{D}}\) đều \( \Rightarrow BI \bot C{\rm{D}}\)
Vậy \(\widehat {AIB}\) là góc phẳng nhị diện \(\left[ {A,C{\rm{D}},B} \right]\).
\(OI = \frac{1}{3}BI = \frac{{a\sqrt 3 }}{6},AO = \sqrt {A{B^2} - B{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\tan \widehat {AIB} = \frac{{AO}}{{OI}} = 2\sqrt 2 \Rightarrow \widehat {AIB} \approx 70,{5^ \circ }\)
\(\Delta AC{\rm{D}}\) đều \( \Rightarrow AI \bot C{\rm{D}}\)
\(\Delta EC{\rm{D}}\) đều \( \Rightarrow EI \bot C{\rm{D}}\)
Vậy \(\widehat {AIE}\) là góc phẳng nhị diện \(\left[ {A,C{\rm{D}},B} \right]\).
\(\widehat {AIE} = {180^ \circ } - \widehat {AIB} = 109,{5^ \circ }\)
