Hoạt động 2
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\). Hãy gọi tên các nửa mặt phẳng có chung bờ \(d\). Các nửa mặt phẳng này chia không gian thành bao nhiêu phần?
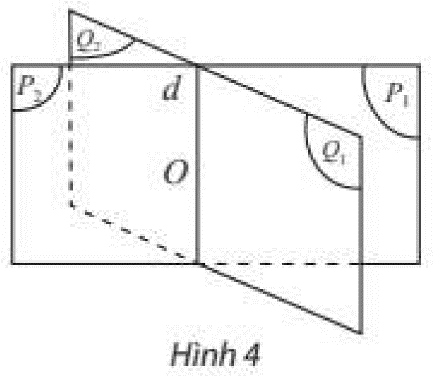

Quan sát hình ảnh và trả lời câu hỏi.

Các nửa mặt phẳng có chung bờ \(d\) là: \(\left( {{P_1}} \right),\left( {{P_2}} \right),\left( {{Q_1}} \right),\left( {{Q_2}} \right)\).
Các nửa mặt phẳng này chia không gian thành 4 phần.
Hoạt động 3
Cho góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\). Gọi \(O\) là một điểm tuỳ ý trên \(d\). \(Ox\) là tia nằm trong \(\left( P \right)\) và vuông góc với \(d\), \(Oy\) là tia nằm trong \(\left( Q \right)\) và vuông góc với \(d\) (Hình 6).
a) Nêu nhận xét về vị trí tương đối giữa \(d\) và \(mp\left( {Ox,Oy} \right)\).
b) Nêu nhận xét về số đo của góc \(xOy\) khi \(O\) thay đổi trên \(d\).
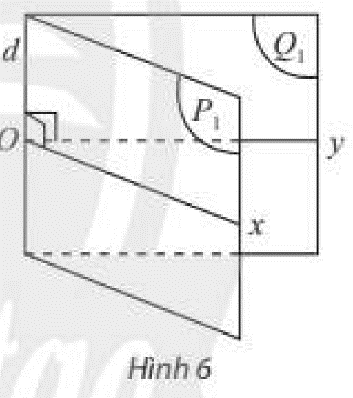

Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).

a) Ta có:
\(\left. \begin{array}{l}d \bot Ox\\d \bot Oy\end{array} \right\} \Rightarrow d \bot mp\left( {Ox,Oy} \right)\)
b) Số đo của góc \(xOy\) không đổi khi \(O\) thay đổi trên \(d\).
Thực hành 2
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).

‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a’\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a’} \right)\).

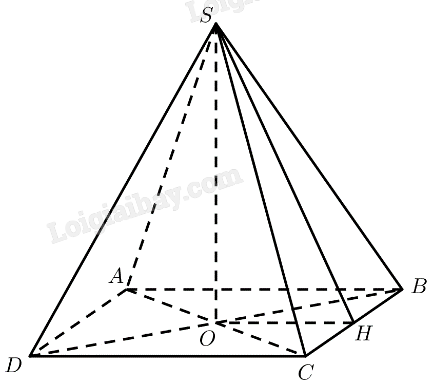
a) Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc phẳng nhị diện \(\left[ {S,BC,O} \right]\).
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
Advertisements (Quảng cáo)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = \frac{a}{2}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SOH\) vuông tại \(O\) có: \(SO = \sqrt {S{C^2} - O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \sqrt 2 \Rightarrow \widehat {SHO} \approx 54,{7^ \circ }\)
b) Ta có:
\(\begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OB\\SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC\end{array}\)
Vậy \(\widehat {BOC}\) là góc phẳng nhị diện \(\left[ {C,SO,B} \right]\).
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow \widehat {BOC} = {90^ \circ }\).
Vận dụng 2
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
(Nguồn: https://en.wikipedia.org/wiki/Memphis Pyramid)


Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

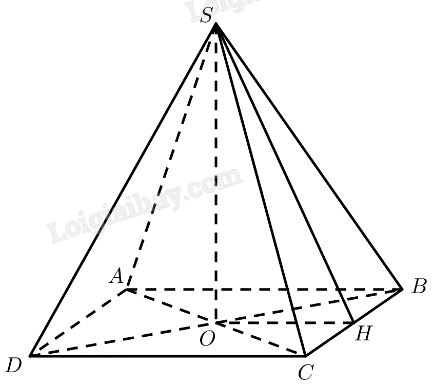
Mô hình hoá kim tự tháp bằng chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy. Vậy \(AB = 180,SO = 98\)
Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc nhị diện tạo bởi mặt bên và mặt đáy.
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = 90\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \frac{{49}}{{45}} \Rightarrow \widehat {SHO} \approx 47,{4^ \circ }\)
Vậy số đo góc nhị diện tạo bởi mặt bên và mặt đáy là \(47,{4^ \circ }\).
