
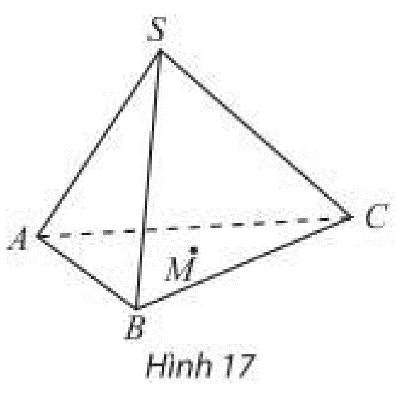
Cho hình chóp \(S.ABC\) và điểm thuộc miền trong tam giác \(ABC\) (Hình 17). Qua \(M\), vẽ đường thẳng \(d\) song song với \(SA\), cắt \(\left( {SBC} \right)\) tại \(N\). Trên hình vẽ, hãy chỉ rõ vị trí của điểm \(N\) và xác định giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {CMN} \right)\).

‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

Advertisements (Quảng cáo)
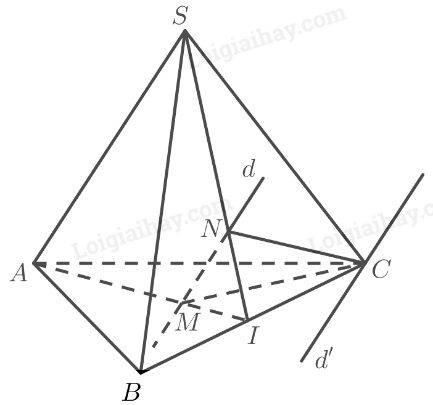
• Gọi \(I\) là giao điểm của \(AM\) và \(BC\). Ta có:
\(\left. \begin{array}{l}d\parallel SA\\M \in d\\M \in \left( {SAI} \right)\end{array} \right\} \Rightarrow d \subset \left( {SAI} \right)\)
Gọi \(N\) là giao điểm của \(d\) và \(SI\). Ta có:
\(\left. \begin{array}{l}N \in d\\N \in SI \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow N = d \cap \left( {SBC} \right)\)
• Ta có:
\(\left. \begin{array}{l}C \in \left( {SAC} \right) \cap \left( {CMN} \right)\\SA\parallel d\\SA \subset \left( {SAC} \right)\\d \subset \left( {CMN} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {CMN} \right)\) là đường thẳng \(d’\) đi qua \(C\), song song với \(SA\) và \(d\).
