
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Hãy ước lượng số trung bình, mốt và tứ phân vị của mẫu số liệu ghép nhóm trên.

Sử dụng công thức tính trung bình cộng, mốt và tứ phân vị của mẫu số liệu ghép nhóm.

Ta có:
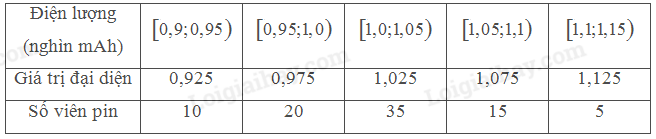
Tổng số viên pin là: \(n = 10 + 20 + 35 + 15 + 5 = 85\).
• Điện lượng trung bình của một số viên pin tiểu sau khi ghép nhóm là:
\(\bar x = \frac{{10.0,925 + 20.0,975 + 35.1,025 + 15.1,075 + 5.1,125}}{{85}} \approx 1,02\left( {mAh} \right)\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\).
Do đó: \({u_m} = 1,0;{n_{m - 1}} = 20;{n_m} = 35;{n_{m + 1}} = 15;{u_{m + 1}} - {u_m} = 1,05 - 1,0 = 0,05\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.0,05 \approx 1,02\left( {mAh} \right)\)
Advertisements (Quảng cáo)
Gọi \({x_1};{x_2};...;{x_{85}}\) là điện lượng của các viên pin được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\left[ {0,9;0,95} \right)}\end{array};{x_{11}},...,{x_{30}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}}\end{array};{x_{31}},...,{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array};\\{x_{66}},...,{x_{80}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,05;1,1} \right)}\end{array}}\end{array};{x_{81}},...,{x_{85}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,1;1,15} \right)}\end{array}}\end{array}}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{43}}\)
Ta có: \(n = 85;{n_m} = 35;C = 10 + 20 = 30;{u_m} = 1,0;{u_{m + 1}} = 1,05\)
Do \({x_{43}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{\frac{{85}}{2} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,02\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 20;C = 10;{u_m} = 0,95;{u_{m + 1}} = 1,0\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}.\left( {1,0 - 0,95} \right) \approx 0,98\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 35;C = 10 + 20 = 30;{u_j} = 1,0;{u_{j + 1}} = 1,05\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,0 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,048\)
