Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(I\) là trung điểm của \(SD\). Hai mặt phẳng \(\left( {IAC} \right)\) và \(\left( {SBC} \right)\) cắt nhau theo giao tuyến \(Cx\). Chứng minh rằng \(Cx\parallel SB\).
Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
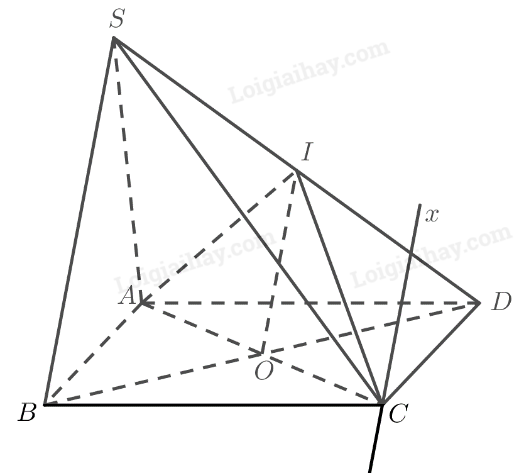
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta có:
\(I\) là trung điểm của \(SD\)
\(O\) là trung điểm của \(BD\) (theo tính chất hình bình hành)
\( \Rightarrow OI\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\( \Rightarrow OI\parallel SB\)
Ta có:
\(\begin{array}{l}Cx = \left( {IAC} \right) \cap \left( {SBC} \right)\\SB = \left( {SB{\rm{D}}} \right) \cap \left( {SBC} \right)\\OI = \left( {IAC} \right) \cap \left( {SB{\rm{D}}} \right)\\SB\parallel OI\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(OI\parallel SB\parallel Cx\).