
Cho hai điểm \(A,B\) nằm ngoài mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(d\) cắt \(\left( \alpha \right)\). Giả sử đường thẳng \(AB\) cắt \(\left( \alpha \right)\) tại điểm \(O\). Gọi \(A’\) và \(B’\) lần lượt là hình chiếu song song của \(A\) và \(B\) trên \(\left( \alpha \right)\) theo phương của đường thẳng \(d\). Ba điểm \(O,A’,B’\) có thẳng hàng không? Vì sao? Chọn \(d\) sao cho:
a) \(A’B’ = AB\);
b) \(A’B’ = 2AB\).

Sử dụng tính chất của phép chiếu song song:
‒ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.

Advertisements (Quảng cáo)
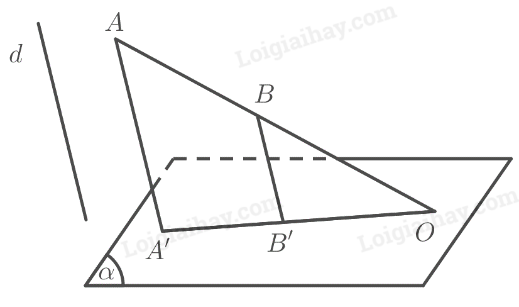
Vì \(O \in \left( \alpha \right)\) nên \(O\) là hình chiếu của chính nó lên mặt phẳng \(\left( \alpha \right)\) theo phương \(d\).
Vì ba điểm \(O,A,B\) thẳng hàng nên ba điểm \(O,A’,B’\) thẳng hàng.
\(AA’\parallel BB’ \Rightarrow \frac{{AB}}{{OA}} = \frac{{A’B’}}{{OA’}} \Leftrightarrow \frac{{A’B’}}{{AB}} = \frac{{OA’}}{{OA}}\)
a) Để \(A’B’ = AB\) thì \(OA’ = OA\).
Vậy đường thẳng \(d\) song song với \(AA’\) và \(OA’ = OA\).
b) Để \(A’B’ = 2AB\) thì \(OA’ = 2OA\).
Vậy đường thẳng \(d\) song song với \(AA’\) và \(OA’ = 2OA\).
