
Cho tứ diện \(ABCD\). Gọi \(E,F,G\) lần lượt là ba điểm trên ba cạnh \(AB,AC,BD\) sao cho \(EF\) cắt \(BC\) tại \(I\left( {I \ne C} \right)\), \(EG\) cắt \(A{\rm{D}}\) tại \(H\left( {H \ne D} \right)\).
a) Tìm giao tuyến của các mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\); \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\).
b) Chứng minh ba đường thẳng \(CD,IG,HF\) cùng đi qua một điểm.

‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
‒ Để chứng minh ba đường thẳng \(CD,IG,HF\) cùng đi qua một điểm, ta chứng minh \(H,F\) và giao điểm của \(CD,IG\) thẳng hàng bằng cách chứng minh ba điểm cùng nằm trên giao tuyến của hai mặt phẳng.

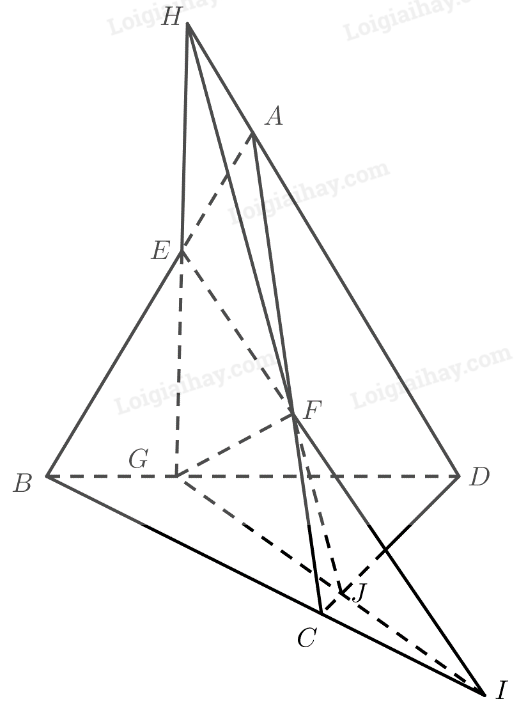
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}G \in \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow G \in \left( {EFG} \right) \cap \left( {BCD} \right)\\\left. \begin{array}{l}I \in EF \subset \left( {EFG} \right)\\I \in BC \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow I \in \left( {EFG} \right) \cap \left( {BCD} \right)\end{array}\)
Advertisements (Quảng cáo)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\) là đường thẳng \(GI\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}F \in \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow F \in \left( {EFG} \right) \cap \left( {ACD} \right)\\\left. \begin{array}{l}H \in EG \subset \left( {EFG} \right)\\H \in A{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow H \in \left( {EFG} \right) \cap \left( {ACD} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\) là đường thẳng \(HF\).
b) Gọi \(J\) là giao điểm của \(CD\) và \(IG\).
Ta có:
\(\left. \begin{array}{l}J \in IG \subset \left( {EFG} \right)\\J \in C{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow J \in \left( {EFG} \right) \cap \left( {ACD} \right)\)
Mà \(F \in \left( {EFG} \right) \cap \left( {ACD} \right),H \in \left( {EFG} \right) \cap \left( {ACD} \right)\) (theo chứng minh phần a).
Do đó ba điểm \(H,F,J\) thẳng hàng.
Vậy ba đường thẳng \(CD,IG,HF\) cùng đi điểm \(J\).
