
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm của \(SO\). Mặt phẳng \(\left( {ICD} \right)\) cắt \(SA,SB\) lần lượt tại \(M,N\).
a) Hãy nói cách xác định hai điểm \(M\) và \(N\). Cho \(AB = a\). Tính \(MN\) theo \(a\).
b) Trong mặt phẳng \(\left( {CDMN} \right)\), gọi \(K\) là giao điểm của \(CN\) và \(DM\). Chứng minh \(SK\parallel BC\parallel AD\).

a) – Để xác định hai điểm \(M\) và \(N\), ta sử dụng tính chất về giao tuyến của hai mặt phẳng và định lí 2 về giao tuyến của ba mặt phẳng.
– Để tính độ dài đoạn thẳng \(MN\), ta sử dụng định lí Medelaus và định lí Thales.
b) Áp dụng định lí 2 về giao tuyến của ba mặt phẳng.

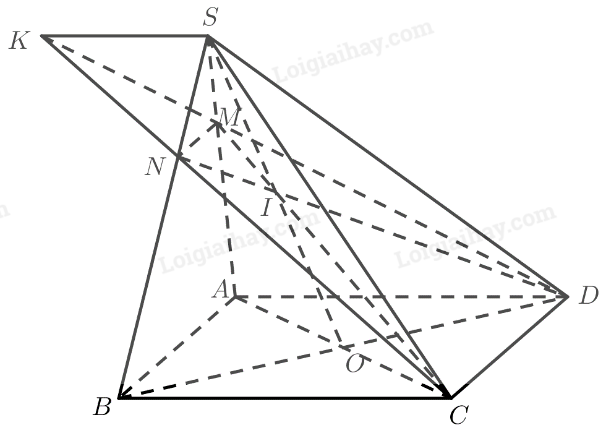
a) • Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {IC{\rm{D}}} \right)\\M \in SA \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow M \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\C \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\end{array}\)
\( \Rightarrow M,I,C\) thẳng hàng.
Do đó \(M\) là giao điểm của \(IC\) và \(SA\).
Advertisements (Quảng cáo)
• Ta có:
\(\begin{array}{l}\left. \begin{array}{l}N \in \left( {IC{\rm{D}}} \right)\\N \in SB \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow N \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\D \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
\( \Rightarrow N,I,D\) thẳng hàng.
Do đó \(N\) là giao điểm của \(I{\rm{D}}\) và \(SB\).
• Ta có:
\(\begin{array}{l}AB = \left( {SAB} \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {IC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {SAB} \right) \cap \left( {IC{\rm{D}}} \right)\\AB\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(AB\parallel C{\rm{D}}\parallel MN\).
Áp dụng định lí Medelaus cho tam giác \(SOA\) với cát tuyến \(CIM\), ta có:
\(\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}\)
Xét tam giác \(SAB\) có \(MN\parallel AB\). Theo định lí Thales ta có:
\(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{1}{3} \Leftrightarrow MN = \frac{1}{3}AB = \frac{a}{3}\)
b) Ta có:
\(\begin{array}{l}BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\SK = \left( {SAD} \right) \cap \left( {SBC} \right)\\AD\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(SK\parallel BC\parallel A{\rm{D}}\).
