
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(M\) là trung điểm của \(CD\), \(\left( P \right)\) là mặt phẳng qua \(M\) song song với \(SA\) và \(BC\). Tìm giao tuyến của \(\left( P \right)\) với các mặt của hình chóp \(S.ABCD\).

Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

Advertisements (Quảng cáo)
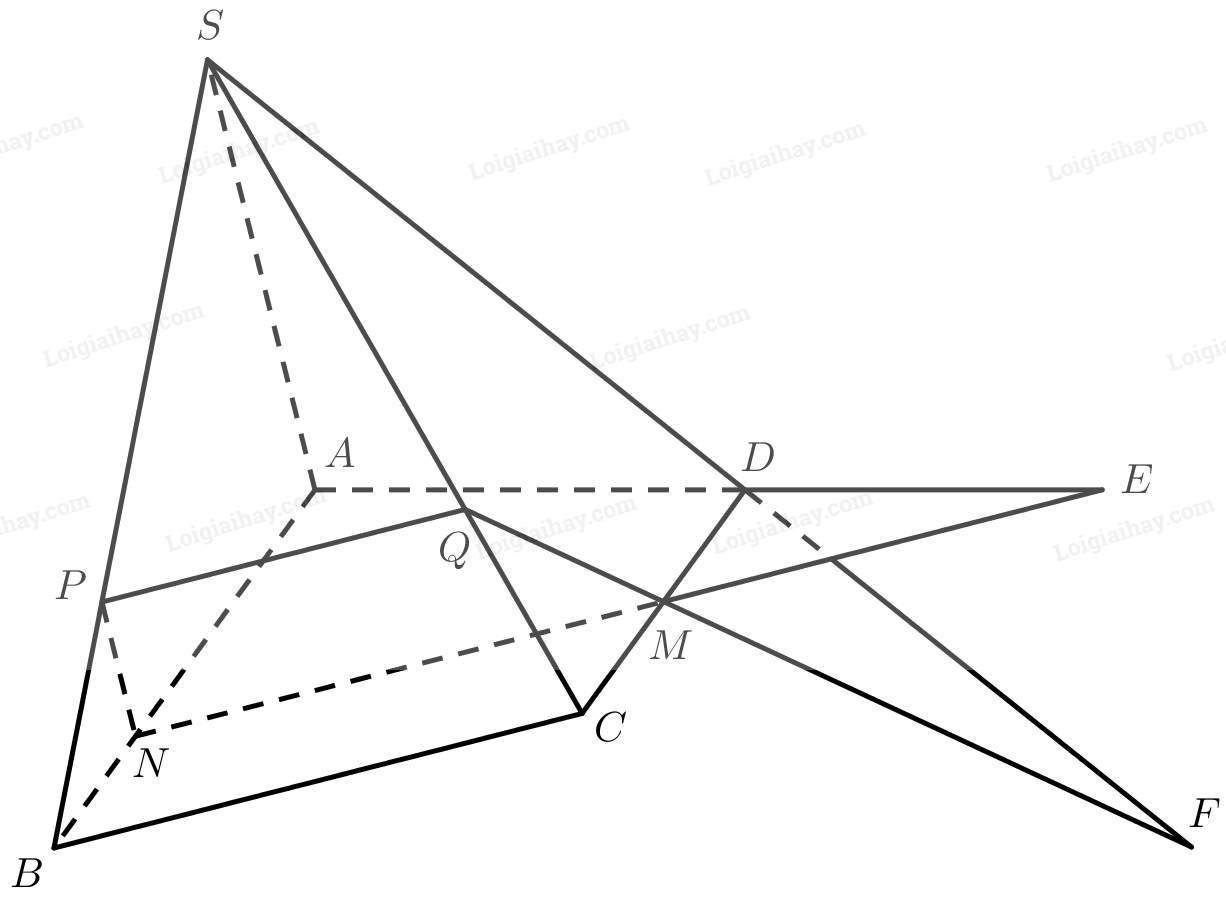
Qua \(M\) dựng đường thẳng song song với \(BC\), cắt \(AB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(SA\), cắt \(SB\) tại \(P\).
Qua \(P\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(Q\).
Vì \(MN\parallel BC,NP\parallel SA\) nên \(\left( {MNPQ} \right) \equiv \left( P \right)\).
Ta có:
\(\begin{array}{l}MN = \left( P \right) \cap \left( {ABC{\rm{D}}} \right)\\NP = \left( P \right) \cap \left( {SAB} \right)\\PQ = \left( P \right) \cap \left( {SBC} \right)\\MQ = \left( P \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Gọi \(E\) là giao điểm của \(A{\rm{D}}\) và \(MN\), \(F\) là giao điểm của \(S{\rm{D}}\) và \(MQ\). Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\E \in MN \subset \left( P \right)\end{array} \right\} \Rightarrow E \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\\left. \begin{array}{l}F \in S{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\F \in MQ \subset \left( P \right)\end{array} \right\} \Rightarrow F \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\ \Rightarrow EF = \left( P \right) \cap \left( {SA{\rm{D}}} \right)\end{array}\)
