
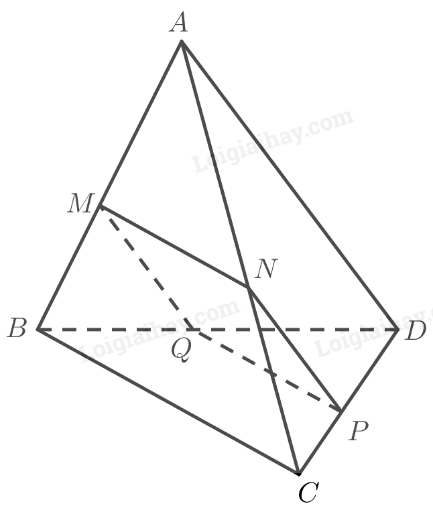
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?

Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC} \right)\\PQ = \left( \alpha \right) \cap \left( {BC{\rm{D}}} \right)\\BC = \left( {ABC} \right) \cap \left( {BC{\rm{D}}} \right)\\MN\parallel BC\end{array}\)
Advertisements (Quảng cáo)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel PQ\parallel BC\) (1).
\(\begin{array}{l}MQ = \left( \alpha \right) \cap \left( {ABD} \right)\\NP = \left( \alpha \right) \cap \left( {AC{\rm{D}}} \right)\\A{\rm{D}} = \left( {ABD} \right) \cap \left( {AC{\rm{D}}} \right)\\MQ\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MQ\parallel NP\parallel A{\rm{D}}\) (2).
Từ (1) và (2) suy ra \(MNPQ\) là hình bình hành.
b) Để \(MNPQ\) là hình thoi thì \(MN = NP\).
Ta có:
\(\begin{array}{l}MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\\NP\parallel A{\rm{D}} \Rightarrow \frac{{NP}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}} \Rightarrow \frac{{MN}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}}\end{array}\)
Ta có:
\(\begin{array}{l}\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1 \Leftrightarrow \frac{{MN}}{{BC}} + \frac{{MN}}{{A{\rm{D}}}} = 1 \Leftrightarrow MN.\left( {\frac{1}{{BC}} + \frac{1}{{A{\rm{D}}}}} \right) = 1\\ \Leftrightarrow MN.\frac{{BC + A{\rm{D}}}}{{BC.A{\rm{D}}}} = 1 \Leftrightarrow MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\end{array}\)
Vậy nếu \(MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\) thì \(MNPQ\) là hình thoi.
