Dựa vào tính chất của đồ thị hàm số \(y = {\log _a}x\). Trả lời bài 6 trang 34 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài tập cuối chương VI. Hình nào vẽ đồ thị của hàm số (y = {log _{frac{1}{2}}}x)?...

Hình nào vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\)?
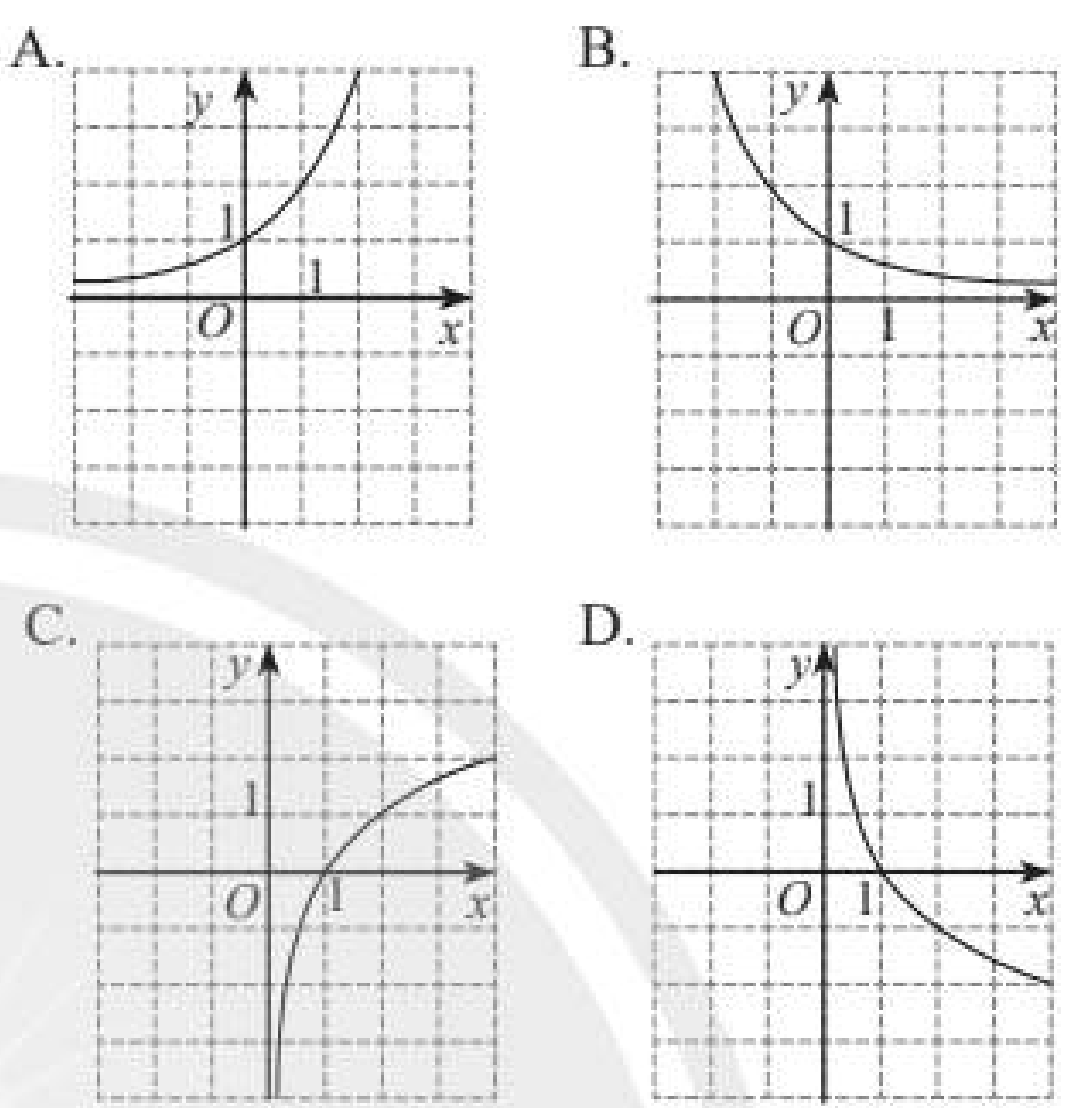

Dựa vào tính chất của đồ thị hàm số \(y = {\log _a}x\).
Advertisements (Quảng cáo)

‒ Hàm số \(y = {\log _{\frac{1}{2}}}x\) nghịch biến trên \(\left( {0; + \infty } \right)\). Loại A, C.
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = + \infty \). Loại B.
Chọn D.
