
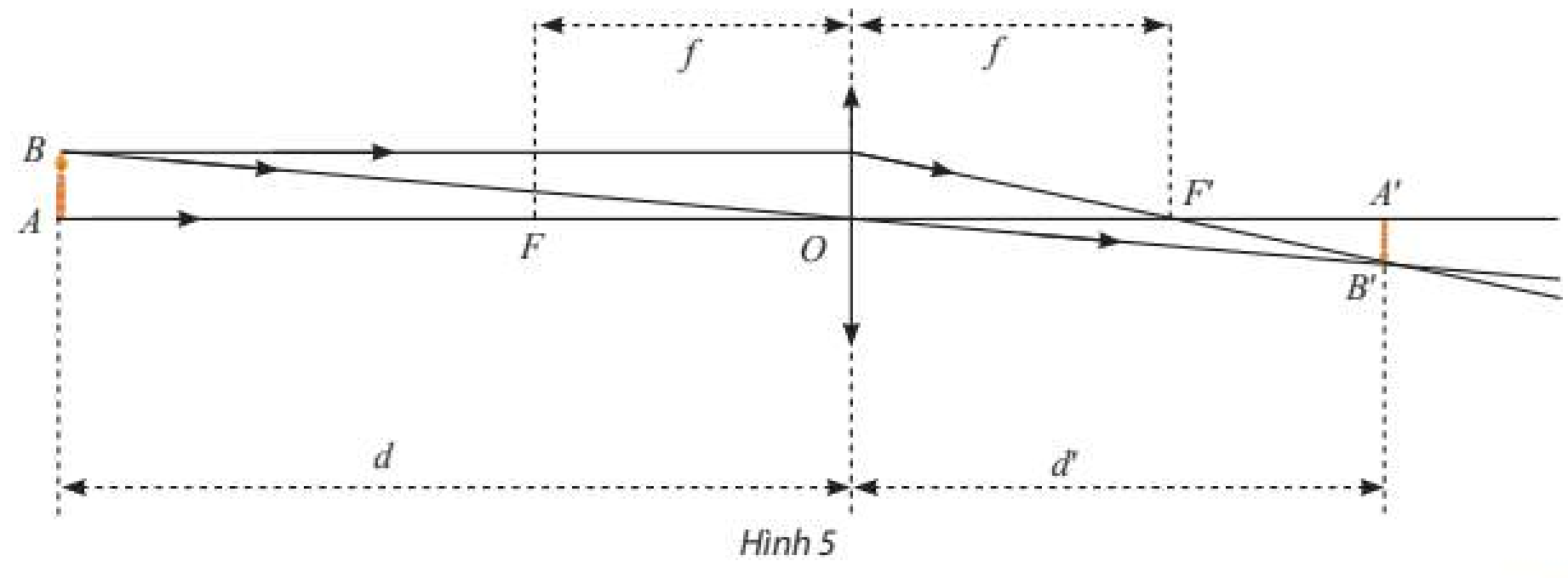
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d’\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d’}} = \frac{1}{f}\) hay \(d’ = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).

a) Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.
Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.
Advertisements (Quảng cáo)
b) Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.

a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F’} \right)\).
