Cho hai hình bình hành và không đồng phẳng. Tìm số giao điểm của mặt phẳng lần lượt với các đường thẳng và .
Hoạt động 1
Cho hai hình bình hành \(ABCD\) và \(ABMN\) không đồng phẳng. Tìm số giao điểm của mặt phẳng \(\left( {ABCD} \right)\) lần lượt với các đường thẳng \(MN,MA\) và \(AC\).
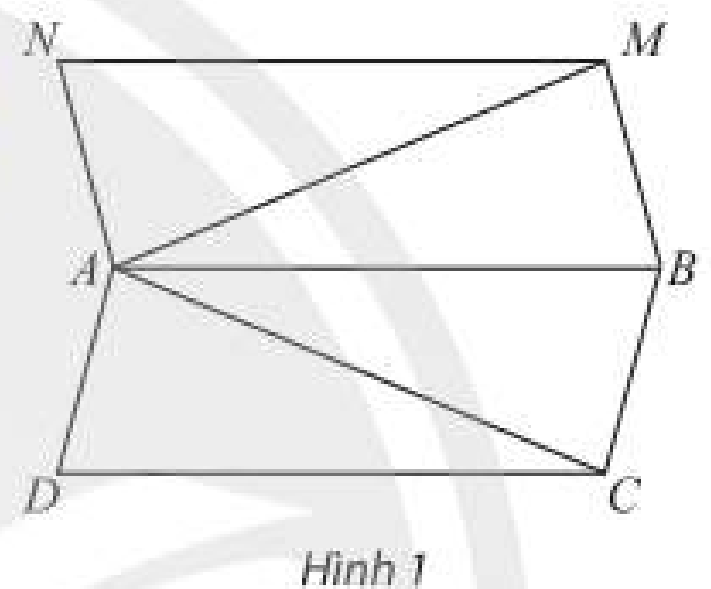

Quan sát hình ảnh, đếm số điểm chung.

‒ Đường thẳng \(MN\) và mặt phẳng \(\left( {ABCD} \right)\) không có giao điểm.
‒ Đường thẳng \(MA\) và mặt phẳng \(\left( {ABCD} \right)\) có 1 giao điểm.
‒ Đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) có vô số giao điểm.
Thực hành 1
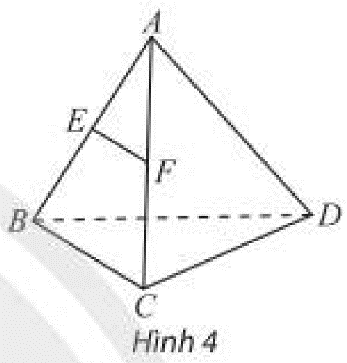
Cho \(E\) và \(F\) lần lượt là trung điểm các cạnh \(AB\) và \(AC\) của tứ diện \(ABC{\rm{D}}\). Xác định vị trí tương đối của các đường thẳng \(BC,AD\) và \(EF\) với mặt phẳng \(\left( {BCD} \right)\).
Advertisements (Quảng cáo)

Dựa vào số điểm chung của đường thẳng và mặt phẳng.

‒ Ta có:
\(\left. \begin{array}{l}B \in \left( {BC{\rm{D}}} \right)\\C \in \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow BC \subset \left( {BC{\rm{D}}} \right)\)
Vậy đường thẳng \(BC\) nằm trong mặt phẳng \(\left( {BCD} \right)\).
‒ Đường thẳng \(AD\) và mặt phẳng \(\left( {BCD} \right)\) có một điểm chung duy nhất \(D\) nên đường thẳng \(AD\) cắt mặt phẳng \(\left( {BCD} \right)\) tại \(D\).
‒ Ta có: \(E\) là trung điểm của \(AB\)
\(F\) là trung điểm của \(AC\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow EF\parallel BC\)
Nếu \(EF\) có điểm chung \(O\) với mặt phẳng \(\left( {BCD} \right)\) thì \(O\) thuộc giao tuyến \(BC\) của hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {BCD} \right)\), suy ra \(EF\) cắt \(BC\) (mâu thuẫn với chứng minh \(EF\parallel BC\) ở trên). Vậy \(EF\parallel \left( {BCD} \right)\).
