Hoạt động 3
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
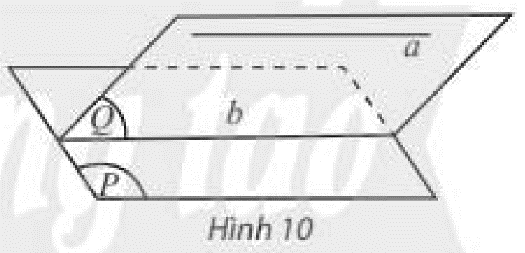

Để xác định vị trí tương đối của hai đường thẳng, ta dựa vào số điểm chung của hai đường thẳng đó.

Ta có: \(a\parallel \left( P \right) \Rightarrow \) Đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung.
\(\left( P \right) \cap \left( Q \right) = b \Rightarrow b \subset \left( P \right)\)
Do đó hai đường thẳng \(a,b\) không có điểm chung.
Hoạt động 4
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b’\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b’\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P’} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b’\) và \(\left( {P’} \right)\); \(\left( P \right)\) và \(\left( {P’} \right)\)?
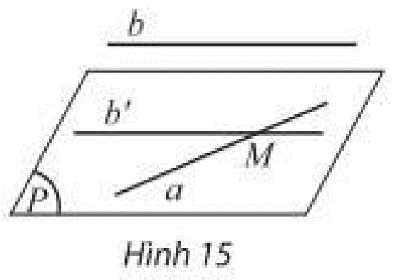

Sử dụng hệ quả 1: Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Nếu qua điểm M thuộc \(\left( P \right)\) ta vẽ đường thẳng \(b\) song song với \(a\) thì \(b\) phải nằm trong \(\left( P \right)\).

a) Ta có:
\(\left. \begin{array}{l}b\parallel b’\\b’ \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P’} \right)\\M \in b’\\b\parallel b’\end{array} \right\} \Rightarrow b’ \subset \left( {P’} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P’} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P’} \right)\\\left. \begin{array}{l}b’ \subset \left( P \right)\\b’ \subset \left( {P’} \right)\end{array} \right\} \Rightarrow b’ = \left( P \right) \cap \left( {P’} \right)\end{array}\)
Do đó \(a\) và \(b’\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P’} \right)\).
Vì \(a\) và \(b’\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P’} \right)\).
Thực hành 3
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
Advertisements (Quảng cáo)
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).
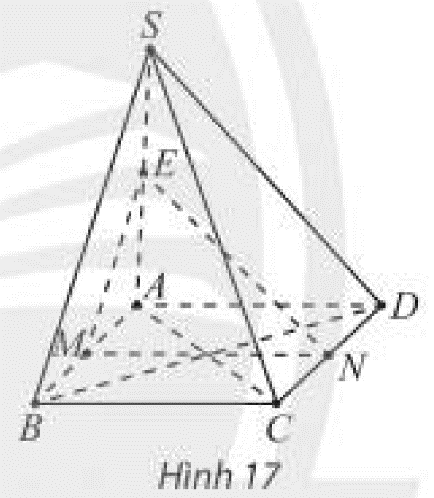

Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.

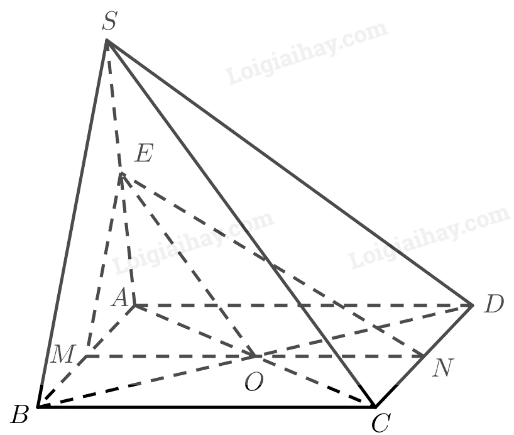
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)
Vận dụng 2
Làm thế nào để đặt cây thước kẻ \(a\) để nó song song các trang của một cuốn sách?

Sử dụng định lí 1: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).

Để đặt cây thước kẻ \(a\) song song các trang của một cuốn sách, ta đặt nó song song với mép cuốn sách.
