Hoạt động 1
Cho hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian. Qua một điểm \(M\) tuỳ ý vẽ \(a’\parallel a\) và vẽ \(b’\parallel b\). Khi thay đổi vị trí của điểm \(M\), có nhận xét gì về góc giữa \(a’\) và \(b’\)?

Quan sát hình ảnh và nhận xét.

Khi thay đổi vị trí của điểm \(M\), góc giữa \(a’\) và \(b’\) không đổi.
Thực hành 1
Cho hình hộp \(ABCD.A’B’C’D’\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA’,A’D’\). Tính góc giữa các cặp đường thẳng:
a) \(MN\) và \(DD’\);
b) \(MN\) và \(CD’\);
c) \(EF\) và \(CC’\).

Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).

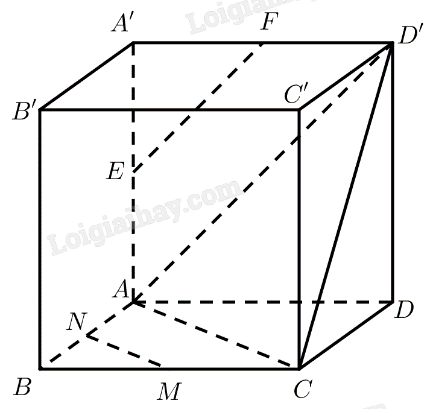
a) Ta có: \(M\) là trung điểm của \(BC\)
\(N\) là trung điểm của \(AB\)
Advertisements (Quảng cáo)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AC\)
Mà \(DD’\parallel AA’\)
\( \Rightarrow \left( {MN,DD’} \right) = \left( {AC,AA’} \right) = \widehat {A’AC} = {90^ \circ }\).
b) Ta có: \(MN\parallel AC\)
\( \Rightarrow \left( {MN,CD’} \right) = \left( {AC,C{\rm{D}}’} \right) = \widehat {AC{\rm{D}}’}\)
Vì \(ABC{\rm{D}},ADD’A’,C{\rm{DD}}'{\rm{C}}’\) là các hình vuông bằng nhau nên các đường chéo của chúng bằng nhau. Vậy \(AC = A{\rm{D}}’ = C{\rm{D}}’\)
\( \Rightarrow \Delta AC{\rm{D}}’\) là tam giác đều \( \Rightarrow \widehat {AC{\rm{D}}’} = {60^ \circ }\).
Vậy \(\left( {MN,CD’} \right) = {60^ \circ }\).
Vận dụng 1
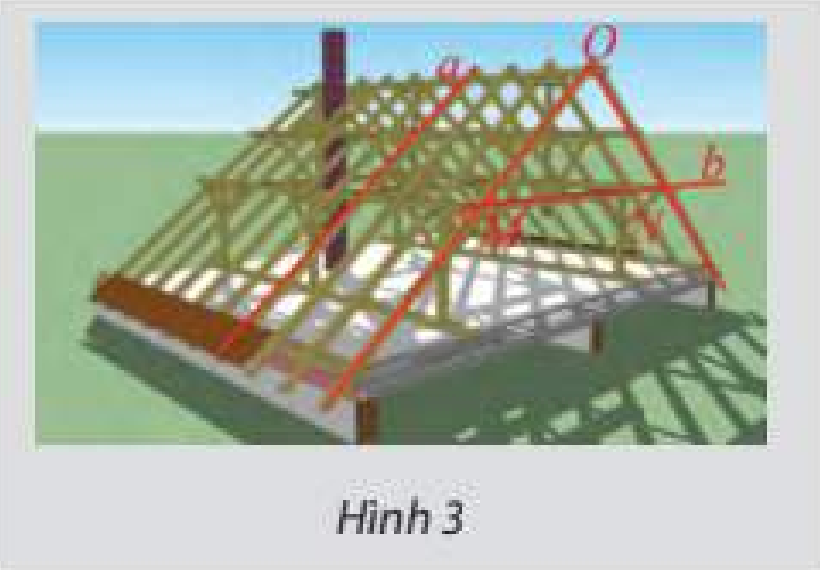
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).

Ta có: \(a\parallel OM \Rightarrow \left( {a,b} \right) = \left( {OM,b} \right) = \widehat {MON} = {90^ \circ }\).
