Hoạt động 2
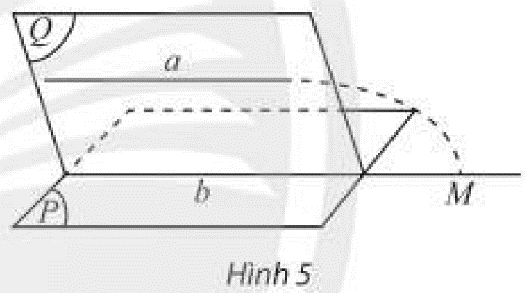
Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\) hay không?

‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt hoặc một đường thẳng chung của hai mặt phẳng.
‒ Để tìm vị trí của điểm \(M\), ta sử dụng tính chất về giao tuyến của hai mặt phẳng.

a) Ta có:
\(\left. \begin{array}{l}b \subset \left( P \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow b = \left( P \right) \cap \left( Q \right)\)
Vậy \(b\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}M \in a\\a \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\)
Lại có: \(M \in \left( P \right)\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in b\).
Vậy \(M\) là một điểm chung của hai đường thẳng \(a\) và \(b\), trái với giả thiết \(a\parallel b\).
Thực hành 2
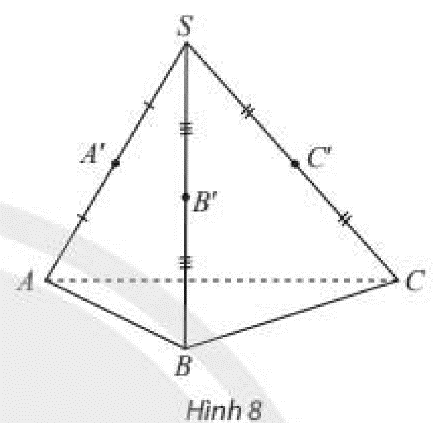
Cho hình chóp \(S.ABC\) có \(A’,B’,C’\) lần lượt là trung điểm của \(SA,SB,SC\). Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng \(\left( {ABC} \right)\).

‒ Để xác định vị trí tương đối của đường thẳng và mặt phẳng, ta dựa vào số điểm chung của đường thẳng và mặt phẳng đó.
‒ Để xác định đường thẳng song song với mặt phẳng, ta sử dụng định lí 1: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
Advertisements (Quảng cáo)
\(A’B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A’B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A’C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A’C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B’A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B’A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B’C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B’C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C’A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C’A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C’B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C’B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A’\) là trung điểm của \(SA\)
\(B’\) là trung điểm của \(SB\)
\( \Rightarrow A’B’\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A’B’\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A’B’\parallel \left( {ABC} \right)\)
\(A’\) là trung điểm của \(SA\)
\(C’\) là trung điểm của \(SC\)
\( \Rightarrow A’C’\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A’C’\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A’C’\parallel \left( {ABC} \right)\)
\(B’\) là trung điểm của \(SB\)
\(C’\) là trung điểm của \(SC\)
\( \Rightarrow B’C’\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B’C’\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B’C’\parallel \left( {ABC} \right)\)
Thực hành 3
Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.


Để xác định vị trí tương đối của đường thẳng và mặt phẳng, ta dựa vào số điểm chung của đường thẳng và mặt phẳng đó.

Các đường thẳng nằm trong mặt phẳng sàn nhà là: mép chân giường, chân tường, mép chân bàn, viền thảm trải sàn,…
Các đường thẳng song song với mặt phẳng sàn nhà là: mép cạnh bàn, mép kệ, mép trần nhà, mép cửa sổ,…
Các đường thẳng cắt mặt phẳng sàn nhà là: cạnh tường, cạnh thẳng đứng của kệ, tủ,…
