Hoạt động 2
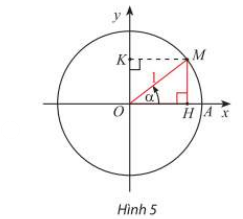
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
b) Chia cả hai vế của biểu thức ở câu a) cho \({\cos ^2}\alpha \) ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho \({\sin ^2}\alpha \) ta được đẳng thức nào?

Dựa vào kiến thức đã học ở phần trên để chứng minh

a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
Advertisements (Quảng cáo)
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)
Thực hành 3
Cho \(\tan \alpha = \frac{2}{3}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Tính \(\cos \alpha \) và \(\sin \alpha \)

Dựa vào công thức đã học ở phần trên để tính

Ta có:
\(\begin{array}{l}{\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow {\left( {\frac{2}{3}} \right)^2} + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{13}}{9}\\ \Rightarrow \cos \alpha = \pm \frac{{3\sqrt {13} }}{{13}}\end{array}\)
Do \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha = - \frac{{3\sqrt {13} }}{{13}}\)
Ta có: \(\begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} \Rightarrow \frac{2}{3} = \sin \alpha :\left( { - \frac{{3\sqrt {13} }}{{13}}} \right)\\ \Rightarrow \sin \alpha = - \frac{{2\sqrt {13} }}{{13}}\end{array}\)
