Giải mục 5 trang 77, 78 Toán 11 tập 1 - Chân trời sáng tạo: Từ đồ thị và bảng trên, có nhận xét gì về giá trị $f\left( x \right)$ khi $x$ dần tới...

Hoạt động 5

Cho hàm số $f\left( x \right) = \frac{1}{{x - 1}}$ có đồ thị như Hình 4.

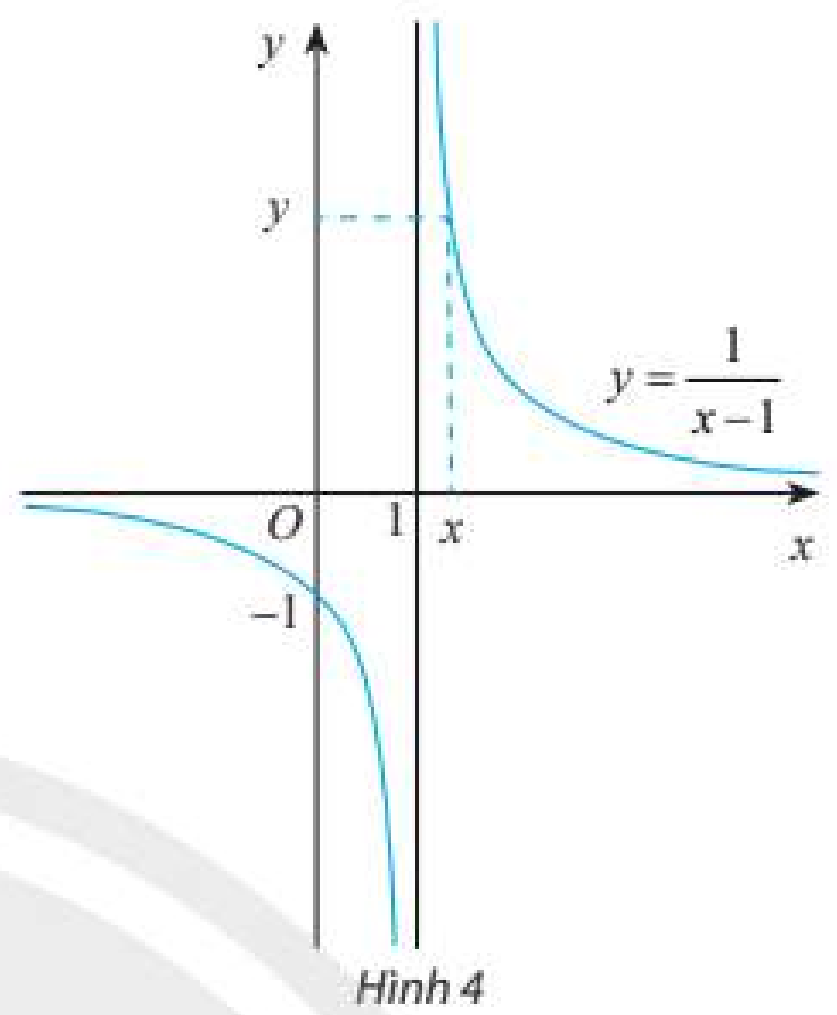
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị $f\left( x \right)$ khi $x$ dần tới 1 phía bên phải?

b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị $f\left( x \right)$ khi $x$ dần tới 1 phía bên trái?

Để điền giá trị vào bảng, ta thay giá trị của $x$ vào hàm số $f\left( x \right) = \frac{1}{{x - 1}}$.

a)

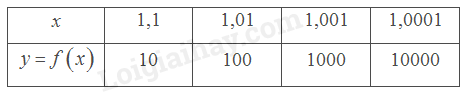
Giá trị $f\left( x \right)$ trở nên rất lớn khi $x$ dần tới 1 phía bên phải.

b)

Giá trị $f\left( x \right)$ trở nên rất bé khi $x$ dần tới 1 phía bên trái.

Thực hành 5

Tìm các giới hạn sau:

a) $\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}}$;

b) $\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right)$.

Bước 1: Đưa hàm số $f\left( x \right)$ về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.

Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.

a) $\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right).\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}$

Ta có: $\mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right) = 2\mathop {\lim }\limits_{x \to {3^ - }} x = 2.3 = 6;\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}} = - \infty$

$\Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = - \infty$

b) $\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } x.\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right)$

Ta có: $\mathop {\lim }\limits_{x \to + \infty } x = + \infty ;\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } 3 - \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 3 - 0 = 3$

$\Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = + \infty$

Vận dụng 2

Xét tình huống ở đầu bài học. Gọi $x$ là hoành độ điểm $H$. Tính diện tích $S\left( x \right)$ của hình chữ nhật $OHMK$ theo $x$. Diện tích này thay đổi như thế nào khi $x \to {0^ + }$ và khi $x \to + \infty$.

− Để tính diện tích $S\left( x \right)$, ta tìm độ dài $OH$ và $OK$ rồi áp dụng công thức tính diện tích hình chữ nhật.

− Để xác định xem diện tích $S\left( x \right)$ thay đổi như thế nào khi $x \to {0^ + }$ và khi $x \to + \infty$, ta tính giới hạn $\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right)$ và $\mathop {\lim }\limits_{x \to + \infty } S\left( x \right)$.

Giả sử điểm $M$ có hoành độ là $x$.

Độ dài $OH$ là hoành độ của điểm $M$. Vậy $OH = x$.

Độ dài $OK$ là tung độ của điểm $M$. Vậy $OK = \frac{1}{{{x^2}}}$.

$S\left( x \right) = OH.OK = x.\frac{1}{{{x^2}}} = \frac{1}{x}$.

$\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty$. Vậy diện tích $S\left( x \right)$ trở nên rất lớn khi $x \to {0^ + }$.

$\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0$. Vậy diện tích $S\left( x \right)$ dần về 0 khi $x \to + \infty$.