
Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:

a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.

Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm
Advertisements (Quảng cáo)
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\).
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\).

14 là tần số lớn nhất nên mốt thuộc nhóm \(\left[ {3;3.5} \right),\) ta có:
\(j = 3,\;{a_3} = 3,\;{m_3} = 14;\;\;{m_2} = 9;\;\;{m_4} = 11,\;h = 0.5\)
Do đó \({M_0} = 3 + \frac{{14 - 9}}{{\left( {14 - 9} \right) + \left( {14 - 11} \right)}} \times 0.5 = 3.31\).
b)
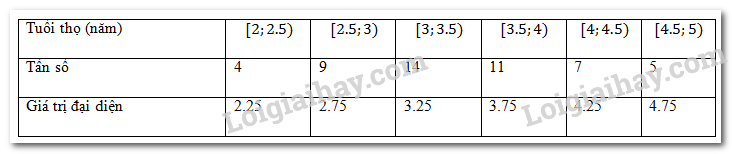
Tuổi thọ trung bình:
\(\bar x = \frac{{4 \times 2.25 + 9 \times 2.75 + 14 \times 3.25 + 11 \times 3.75 + 7 \times 4.25 + 5 \times 4.75}}{{50}} = 3.48\).
