
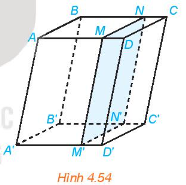
Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng song song với mặt bên (ABB’A’) của hình hộp và cắt các cạnh AD, BC, A’D, B’C’ lần lượt tại M, N, M’, N’ (H.4.54).
Chứng minh rằng ABNM.A’B’N’M” là hình hộp.

Hình lăng trụ tứ giác có hai đáy là hình bình hành được gọi là hình hộp.

\( - \;\)Ta có \(\left( {ABB’C’} \right)\;//\;\left( {MNN’M’} \right),\;\left( {ADD’A’} \right) \cap \left( {ABB’A’} \right) = AA’,\left( {ADD’A’} \right) \cap \left( {MNN’M’} \right) = MM’\)
Advertisements (Quảng cáo)
suy ra AA’//MM’
Tương tự, BB’ // NN’
ABNM.A’B’N’M’ có các cạnh bên đôi một song song, (ABNM) //(A’B’N’M’)
Suy ra ABNM.A’B’C’M’ là hình lăng trụ.
\( - \;\)Ta có: \(\left( {ABB’C’} \right)\;//\;\left( {MNN’M’} \right),\;\left( {ABNM} \right) \cap \left( {ABB’A’} \right) = AB,\left( {ABNM} \right) \cap \left( {MNN’M’} \right) = MN\)
Suy ra AB//MN.
Ta có có AB // MN, BN// AM nên tứ giác ABNM là hình bình hành.
Do đó ABNM.A’B’C’M’ là hình hộp.
