Hoạt động 5
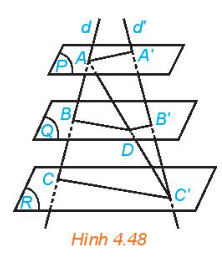
Cho mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ (C khác C’). Gọi D là giao điểm của AC’ và (Q) (H.4.48)
a) Các cặp đường thẳng BD và CC’, B’D và AA’ có song song với nhau không?
b) Các tỉ số \(\frac{{AB}}{{BC}},\frac{{AD}}{{DC’}}\) và \(\frac{{A’B’}}{{B’C’}}\) có bằng nhau không?

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.

a) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC’) với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC’
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C’AA’) với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B’D // AA’
b) Xét tam giác ACC’ ta có BD // CC’ suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC’}}\)
Advertisements (Quảng cáo)
Xét tam giác C’AA’ ta có B’D // AA’ suy ra \(ADDC’ = A’B’B’C’\)
Do đó, \(\frac{{AB}}{{BC’}} = \frac{{AD}}{{DC’}} = \frac{{A’B’}}{{B’C’}}\)
Luyện tập 4
Trong HĐ5, cho AB = 2cm, BC = 4cm và A’B’ =3cm. Tính độ dài của đoạn thẳng B’C’.

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.

Áp dụng định lí Thales cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d’ ta có:
\(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}}\) suy ra \(\frac{2}{4} = \frac{3}{{B’C’}}\)
=>B’C’ = 6 (cm).
