khi cắt tứ diện bằng một mặt phẳng thì thiết diện nhận được có thể là những hình nào sau đây ?
a. Hình thang
b. Hình bình hành
c. Hình thoi

a.
Có thể cắt tứ diện bằng một mặt phẳng để thiết diện là hình thang, ví dụ như mặt phẳng đi qua M, N (M, N là hai điểm lần lượt nằm trên hai cạnh AB, BC) và song song với BD
b.
Advertisements (Quảng cáo)

Có thể cắt tứ diện bằng một mặt phẳng để thiết diện là hình bình hành, ví dụ như mặt phẳng đi qua điểm M nằm trên cạnh AB và song song với hai đường thẳng BD và AC.
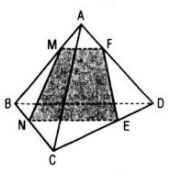
c. Có thể. Giả sử mặt phẳng cắt là (P) qua điểm M thuộc đoạn AB, song song với BD và AC. Khi đó thiết diện là hình bình hành MNEF.
Ta có:
\(\eqalign{ & {{MF} \over {BD}} = {{AM} \over {AB}} \Rightarrow MF = {{BD.AM} \over {AB}} \cr & {{MN} \over {AC}} = {{MB} \over {AB}} \Rightarrow MN = {{AC.MB} \over {AB}} \cr} \)
Tứ giác MNEF là hình thoi
\( \Leftrightarrow MF = MN \Leftrightarrow BD.AM = AC.MB \)
\(\Leftrightarrow {{AM} \over {MB}} = {{AC} \over {BD}}.\left( * \right)\)
Vậy với M xác định ở (*) thì mp(P) qua M và song song với AC, BD sẽ cắt tứ diện theo một thiết diện là hình thoi.
