36. Trang 57 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của cạnh SC; (P) là mặt phẳng qua AM và song song với BD.
a) Xác định thiết diện của hình chóp khi cắt bởi mp(P).
b) Gọi E và F lần lượt là giao điểm của (P) với các cạnh SB và SD. Hãy tìm tỉ số diện tích của tam giác SME với tam giác ABC và tỉ số diện tích của tam giác SMF với tam giác SCD.
c) Gọi K là giao điểm của ME với CB, J là giao điểm của MF và CD. Hãy chứng minh ba điểm K, A, J nằm trên một đường thẳng song song với EF và tìm tỉ số \({{EF} \over {KJ}}.\)

a) Gọi I là giao điểm của SO và AM (O là giao điểm của AC và BD). Vì BD // (P) nên mặt phẳng (SBD) chứa BD cắt (P) theo giao tuyến qua I và song song với BD. Gọi E và F lần lượt là giao điểm của giao tuyến này với các cạnh SB và SD thì E và F lần lượt là giao điểm của SB và SD với mặt phẳng (P).
Vậy thiết diện là tứ giác AEMF.
Advertisements (Quảng cáo)
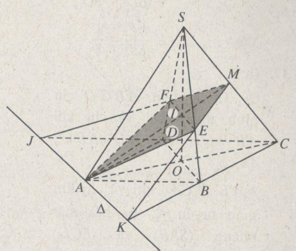
b) Dễ thấy I là trọng tâm tam giác SAC, ta có:
\({{SE} \over {SB}} = {{SF} \over {SD}} = {{SI} \over {SO}} = {2 \over 3}.\)
Do đó:
\(\eqalign{
& {{{S_{SME}}} \over {{S_{SBC}}}} = {{SM} \over {SC}}.{{SE} \over {SB}} = {1 \over 2}.{2 \over 3} = {1 \over 3} \cr
& {{{S_{SMF}}} \over {{S_{SCD}}}} = {{SM} \over {SC}}.{{SF} \over {SD}} = {1 \over 2}.{2 \over 3} = {1 \over 3} \cr} \)
c) Dễ thấy K, A, J là ba điể chung của hai mặt phẳng (P) và (ABCD) nên chúng nằm trên giao tuyến của hai mặt phẳng này. Vì BD // (P) và \(BD \subset \left( {ABCD} \right)\) nên \(\Delta //BD \Rightarrow \Delta //EF.\) Ta có:
\({{EF} \over {BD}} = {{SI} \over {SO}} = {2 \over 3};\,KJ = 2BD.\)
Vậy \({{EF} \over {KJ}} = {1 \over 3}.\)
