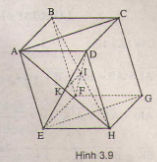
Bài 10. Cho hình hộp \(ABCD.EFGH\). Gọi \(K\) là giao điểm của \(AH\) và \(DE\), \(I\) là giao điểm của \(BH\) và \(DF\). Chứng minh ba véctơ \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.

(H.3.9) Chứng minh giá của các véctơ \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) song song với mặt phẳng \((ABCD)\) chứa véctơ \(\overrightarrow{AC}\). Từ đó suy ra ba véctơ đồng phẳng.
\(I=BH\cap DF\) là giao điểm của hai đường chéo hình bình hành \(BDHF\) do đó \(I\) là trung điểm của \(BH\) (1)
\(K\) là giao điểm của hai đường chéo hình bình hành \(ADHE\) do đó \(K\) là trung điểm của \(AH\) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra \(KI\) là đường trung bình của tam giác \(ABH\). Do đó \(KI//AB\) suy ra \(KI//(ABCD)\) (*)
Ta có: \(BCGF\) là hình bình hành nên \(FG//BC\) suy ra \(FG//(ABCD)\) (2*)
Từ (*) và (2*) suy ra: \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.
 của
của
