Bài 2 trang 53 sách giáo khoa hình học lớp 11: Bài 1. Đại cương về đường thẳng và mặt phẳng. Gọi M là giao điểm của đường thẳng d và mặt phẳng (α ). Chứng minh M là điểm chung của (α ) với một mặt phẳng bất kì chứa d
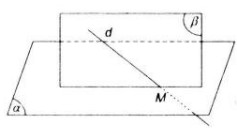
Bài 2. Gọi \(M\) là giao điểm của đường thẳng \(d\) và mặt phẳng \((α )\). Chứng minh \(M\) là điểm chung của \((α )\) với một mặt phẳng bất kì chứa \(d\)

Advertisements (Quảng cáo)
Hiển nhiên \(M ∈ (α )\) , Gọi \((β)\) là mặt phẳng bất kì chứa \(d\), ta có
\(\left\{ \matrix{
M \in d \hfill \cr
d \subset (\beta ) \hfill \cr} \right. \Rightarrow M \in (\beta )\)
Vậy \(M\) là điểm chung của \((α )\) và mọi mặt phẳng \((β)\) chứa \(d\).
