Bài 8. Cho tứ diện đều \(ABCD\) cạnh \(a\). Tính khoảng cách giữa hai cạnh đối diện của tứ diện.

(H.3.69)
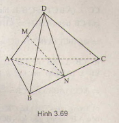
Gọi \(M, N\) lần lượt là trung điểm của \(AD\) và \(BC\),
\(\Delta BAC = \Delta BDC(c.c.c)\) \( \Rightarrow AN = DN\) (hai đường trung tuyến tương ứng của hai tam giác bằng nhau)
Tam giác \(AND\) cân tại \(N\), nên \(MN\) vừa là đường trung tuyến đồng thời là đường cao do đó \(MN\bot AD\) (1)
Advertisements (Quảng cáo)
Chứng minh tương tự ta được: \(MN\bot BC\) (2)
Từ (1) và (2) suy ra \(MN\) là đường vuông góc chung của \(BC\) và \(AD\)
Tam giác \(ABC\) đều nên \(AN={{a\sqrt 3 } \over 2}\)
Áp dụng định lí Pytago vào tam giác vuông \(AMN\) ta có:
\(A{N^2} = M{N^2} + A{M^2}\)
\(MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {{{3{a^2}} \over 4} - {{{a^2}} \over 4}} = {{a\sqrt 2 } \over 2}\)
