Cho ABC là tam giác đều cạnh a. Trên đường thẳng At vuông góc với mp(ABC) lấy điểm S với AS = b.
a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, b.
b) Hz là đường thẳng đi qua trực tâm H của tam giác SBC và vuông góc với mp(SBC). Chứng minh rằng khi S di động trên At thì đường thẳng Hz luôn đi qua một điểm cố định.

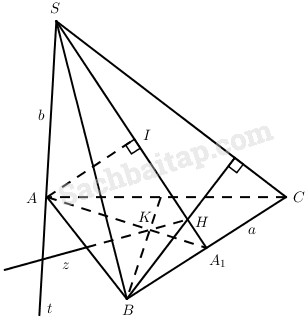
a) Gọi A1 là trung điểm của BC thì \(BC \bot mp\left( {SA{A_1}} \right)\), từ đó \(\left( {SA{A_1}} \right) \bot \left( {SBC} \right)\).
Kẻ đường cao AI của tam giác SAA1 thì \(AI \bot \left( {SBC} \right)\). Từ đó, khoảng cách từ A đến mp(SBC) bằng AI.
Advertisements (Quảng cáo)
Ta có \(AI = {{AS.A{A_1}} \over {S{A_1}}} = {{b.{{a\sqrt 3 } \over 2}} \over {\sqrt {{b^2} + {{3{a^2}} \over 4}} }}\).
Vậy \(AI = {{ab\sqrt 3 } \over {\sqrt {3{{\rm{a}}^2} + 4{b^2}} }}\).
b) Vì H là trực tâm tam giác SBC nên H thuộc SA1. Do \(\left( {SA{A_1}} \right) \bot \left( {SBC} \right)\) và \(H{\rm{z}} \bot \left( {SBC} \right)\) nên Hz nằm trong mp(SAA1). Gọi K là giao điểm của Hz và AA1, ta có \(KH \bot \left( {SBC} \right),BH \bot SC\) nên \(KB \bot SC\) (định lí ba đường vuông góc).
Mặt khác \(SA \bot \left( {ABC} \right),BK \bot SC\) nên \(BK \bot AC\) (định lí ba đường vuông góc). Như vậy K là trực tâm của tam giác ABC.
Vậy khi S di động trên đường thẳng At vuông góc với mp(ABC) thì đường thẳng Hz đi qua điểm cố định là trực tâm K của tam giác ABC.
