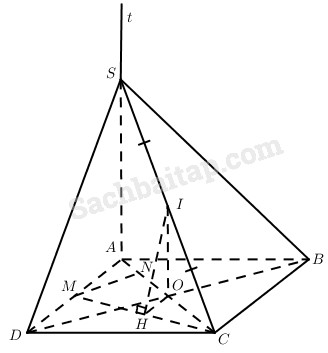
Trên cạnh AD của hình vuông ABCD cạnh a, ta lấy điểm M với AM = x (0 < x < AD) và trên nửa đường thẳng At vuông góc với mặt phẳng (ABCD) lấy điểm S sao cho AS = y.
a) Tính khoảng cách từ điểm M đến mặt phẳng (SAC).
b) Gọi I là trung điểm của SC và H là hình chiếu của I trên CM. Chứng minh rằng điểm H thuộc đường tròn cố định khi M chạy trên AD và S chạy trên At.

Advertisements (Quảng cáo)
a) Gọi O là giao điểm của AC và BD thì \(DB \bot \left( {SAC} \right)\). Kẻ MN song song với \(DB\left( {N \in AC} \right)\) thì \(MN \bot \left( {SAC} \right)\), do đó khoảng cách từ M đến mp(SAC) bằng MN. Dễ thấy:
\(MN = {{AM} \over {\sqrt 2 }} = {x \over {\sqrt 2 }}\).
b) Ta có IO // SA, do \(SA \bot \left( {ABC{\rm{D}}} \right)\) nên \(I{\rm{O}} \bot \left( {ABC{\rm{D}}} \right)\).
Do \(IH \bot MC\) nên \(HO \bot HC\) (định lí ba đường vuông góc). Vậy \(\widehat {OHC} = {90^0}\), tức là H thuộc đường tròn đường kính OC nằm trong mặt phẳng chứa hình vuông ABCD.
