Cắt hình lập phương bằng một mặt phẳng (P) đi qua một đường chéo của hình lập phương. Phải chọn (P) như thế nào để thiết diện thu được có diện tích nhỏ nhất.

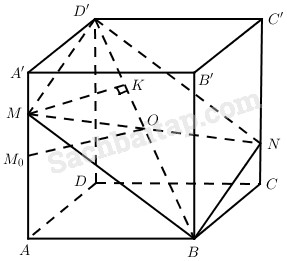
Xét (P) là mặt phẳng chứa một đường chéo, chẳng hạn đường chéo BD’ của hình lập phương.
Nếu (P) chứa D’A’ thì thiết diện có diện tích là \({a^2}\sqrt 2 .\)
Tương tự, nếu (P) chứa D’C’ hoặc D’D thì thiết diện cũng có diện tích là \({a^2}\sqrt 2 \).
Ta xét (P) cắt AA’ tại điểm M. Gọi O là tâm hình lập phương thì MO cắt CC’ tạo N. Do đó thiết diện của hình lập phương khi cắt bởi (P) là BMD’N, đó là hình bình hành.
Ta có \({S_{BM{\rm{D}}’N}} = B{\rm{D}}’.MK = d.MK\)
Advertisements (Quảng cáo)
(d là độ dài đường chéo của hình lập phương).
Vậy \({S_{BM{\rm{D}}’N}}\) nhỏ nhất khi và chỉ khi MK nhỏ nhất, tức MK là đường vuông góc chung của BD’ và AA’. Dễ thấy OM0 là đường vuông góc chung của BD’ và AA’, trong đó M0 là trung điểm của AA’; \(O{M_0} = {{a\sqrt 2 } \over 2}\). Vậy lúc đó:
\({S_{BMD’N}} = a\sqrt 3 .{{a\sqrt 2 } \over 2} = {{{a^2}\sqrt 6 } \over 2}\)
Chú ý. Khi (P) cắt A’B’ hoặc B’C’ thì cách giải quyết câu toán cũng như trên và ta có diện tích thiết diện nhỏ nhất trong trường hợp đó cũng là \({{{a^2}\sqrt 6 } \over 2}\).
Dễ thấy \({{{a^2}\sqrt 6 } \over 2} < {a^2}\sqrt 2 .\)
Vậy nếu (P) qua đường chéo BD’ và qua trung điểm một cạnh của hình lập phương không đi qua B và D’, thì diện tích thiết diện nhỏ nhất và có giá trị bằng \({{{a^2}\sqrt 6 } \over 2}\).
