Bài 8. Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat{BAC}=\widehat{BAD}=60^{0}.\) Chứng minh rằng:
a) \(AB ⊥ CD\);
b) Nếu \(M, N\) lần lượt là trung điểm của \(AB\) và \(CD\) thì \(MN ⊥ AB\) và \(MN ⊥ CD\).

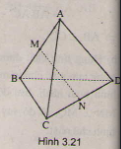
(h.3.21)
a) \(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}(\overrightarrow{AD}-\overrightarrow{AC})\)
\(=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\)
\(=AB.AD.\cos\widehat{BAD}-AB.AC.\cos\widehat{BAC} =0\)
Advertisements (Quảng cáo)
\(\Rightarrow AB ⊥ CD\).
b) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN},\) (1)
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\) (2)
Cộng (1) với (2) theo vế với vế ta được: \(\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{BC})=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AC}-\overrightarrow{AB}).\)
Ta có \(\overrightarrow{AB}.\overrightarrow{MN}={1 \over 2}\overrightarrow {AB} .(\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} )\)
\(= {1 \over 2}(\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - A{B^2})\)
\(= {1 \over 2}(AB.AD.\cos\widehat{BAD}+AB.AC.\cos\widehat{BAC}-AB^2)\)
\(={1 \over 2}(AB.AD.\cos60^0+AB.AC.\cos60^0-AB^2)\)
\(={1 \over 2}\left({1 \over 2}AB^2+{1 \over 2}AB^2-AB^2\right)=0\) \(\Rightarrow AB ⊥ MN\).
Chứng minh tương tự ta được: \(CD ⊥ MN\).
