
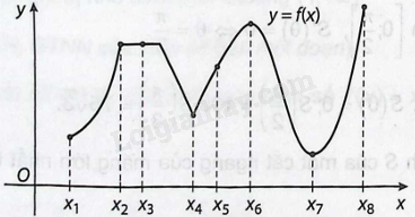
Sử dụng đồ thị dưới đây, xác định xem hàm số \(y = f\left( x \right)\) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}\) hay không.

Quan sát đồ thị kết hợp với định nghĩa cực trị, giá trị lớn nhất, nhỏ nhất của hàm số để đưa ra kết luận.

Ta có hàm số \(y = f\left( x \right)\) xác định trên \(\left[ {{x_1};{x_8}} \right]\). Từ đồ thị ta có:
Advertisements (Quảng cáo)
+ \(f\left( x \right) \le f\left( {{x_8}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_8} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_8}} \right)\). Do đó hàm số đạt giá trị lớn nhất tại điểm \({x_8}\).
+ \(f\left( x \right) \ge f\left( {{x_7}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_7} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_7}} \right)\). Do đó hàm số
đạt giá trị nhỏ nhất tại điểm \({x_7}\).
Ta có hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ {{x_1};{x_8}} \right]\).
+ Gọi \({h_1} = \frac{{{x_5} - {x_4}}}{2}\) , ta thấy \({h_1}\) dương. Vì \(f\left( x \right) > f\left( {{x_4}} \right)\) với mọi \(x \in \left( {{x_4} - {h_1};{x_4} + {h_1}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_4}\) nên hàm số đạt cực tiểu tại điểm \({x_4}\).
+ Tương tự, gọi \({h_2} = \frac{{{x_8} - {x_7}}}{2}\) , ta thấy \({h_2}\) dương. Vì \(f\left( x \right) > f\left( {{x_7}} \right)\) với mọi \(x \in \left( {{x_7} - {h_2};{x_7} + {h_2}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_7}\) nên hàm số đạt cực tiểu tại điểm \({x_7}\).
+ Gọi \({h_3} = \frac{{{x_6} - {x_5}}}{2}\) , ta thấy \({h_3}\) dương. Vì \(f\left( x \right)
