
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = 3{x^4} - 4{x^3}\);
b) \(y = \frac{{{x^2}}}{{x - 1}},x > 1\).

- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số. Từ bảng biến thiên ta tìm được giá trị lớn nhất, nhỏ nhất.

a) Tập xác định: \(\mathbb{R}\)
Advertisements (Quảng cáo)
Ta có \(y’ = 12{x^3} - 12{x^2}\). Khi đó \(y’ = 0 \Leftrightarrow 12{x^3} - 12{x^2} = 0 \Leftrightarrow 12{x^2}\left( {x - 1} \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
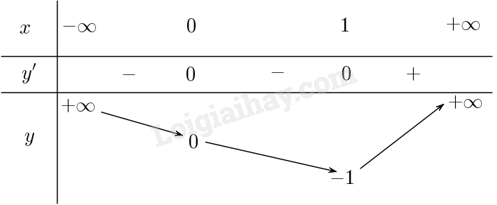
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} y = y\left( 1 \right) = - 1\); Hàm số không có giá trị lớn nhất.
b) Tập xác định: \(\left( {1; + \infty } \right)\)
Ta có \(y’ = \frac{{2x\left( {x - 1} \right) - {x^2} \cdot 1}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\). Khi đó \(y’ = 0 \Leftrightarrow \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x = 2\) (vì \(x > 1\))
Lập bảng biến thiên của hàm số:
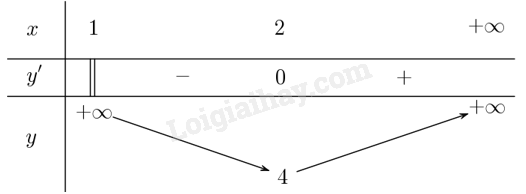
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( 2 \right) = 4\). Hàm số không có giá trị lớn nhất trên khoảng \(\left( {1; + \infty } \right)\).
