
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có \(80000\) con. Sau \(t\) năm số lượng quần thể cá nói trên được xác định bởi
\(N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\) (nghìn con).
a) Khảo sát sự biến thiên của hàm số \(y = N\left( t \right)\).
b) Số lượng tối đa có thể chứa của quần thể cá là bao nhiêu?

Ý a: Khảo sát sự biến thiên của hàm số \(y = N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\).
Ý b: Tìm giá trị lớn nhất của hàm số.

a) Xét hàm số \(y = N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\).
Advertisements (Quảng cáo)
Tập xác định: \(\left[ {0; + \infty } \right)\).
Sự biến thiên: \(y’ = N’\left( t \right) = {\left[ {\frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}} \right]^\prime } = \frac{{56}}{{{{\left( {1 + 0,05t} \right)}^2}}} > 0\) với mọi \(t \ge 0\).
+ Hàm số đồng biến trên khoảng \(\left[ {0; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } N\left( t \right) = 1200\)
+ Bảng biến thiên:
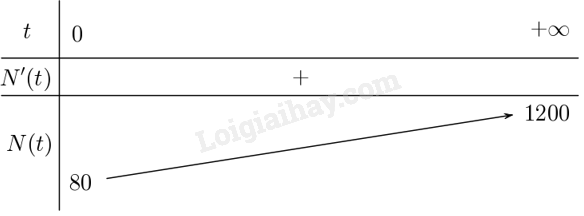
b) Hồ có số lượng cá tối đa khi hàm số \(N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\) đạt giá trị lớn nhất.
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số là \(1200\).
Vậy hồ có thể chứa tối đa 1200 nghìn con hay 1200000 con cá.
