
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ - x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?

+ Tìm công thức \(R’\left( x \right)\).
+ Tìm \(x\) để \(R’\left( x \right)\) đạt giá trị lớn nhất.

Hàm biểu thị tốc độ bán hàng là \(R’\left( x \right) = \frac{{25000{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^2}}},{\rm{ x}} \ge 0\).
Advertisements (Quảng cáo)
Tốc độ bán hàng tối đa khi \(R’\left( x \right)\) đạt giá trị lớn nhất, ta cần tìm giá trị lớn nhất của \(R’\left( x \right)\) trên \(\left[ {0; + \infty } \right)\).
Ta có \(R”\left( x \right) = - 25000 \cdot \frac{{{e^{ - x}}{{\left( {1 + 5{e^{ - x}}} \right)}^2} + {e^{ - x}} \cdot 2\left( {1 + 5{e^{ - x}}} \right) \cdot 5{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^4}}} = \frac{{25000\left( {5{e^{ - x}} - 1} \right)}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^3}}}\)
Khi đó \(R”\left( x \right) = 0 \Leftrightarrow \frac{{25000\left( {5{e^{ - x}} - 1} \right)}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^3}}} = 0 \Leftrightarrow \left( {5{e^{ - x}} - 1} \right) = 0 \Leftrightarrow x = \ln 5\).
Lập bảng biến thiên
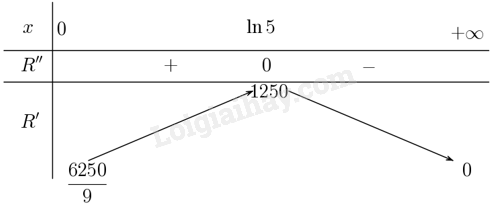
Từ bảng biến thiên suy ra \(R’\) đạt giá trị lớn nhất tại \(x = \ln 5 \approx 1,61\). Vậy tốc độ bán hàng đạt tối đa vào thời điểm năm thứ hai.
