
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên dưới đây:
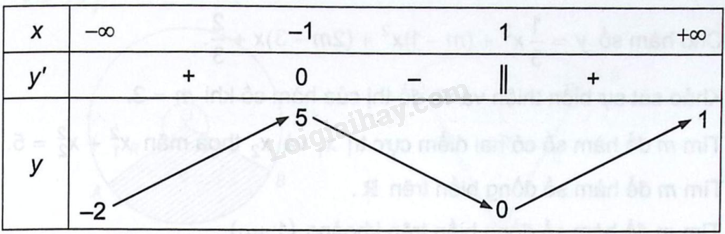
Khẳng định nào dưới đây là sai?
A. Giá trị nhỏ nhất của hàm số bằng -2.
B. Giá trị lớn nhất của hàm số bằng 5.
C. Đồ thị hàm số có hai tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là \(\left( {1;0} \right)\).
Advertisements (Quảng cáo)

Quan sát bảng biến thiên và vận dụng các kiến thức về cực trị, giá trị lớn nhất, nhỏ nhất, tiệm cận đã học.

Đáp án: A.
Từ bảng biến thiên suy ra hàm số đạt giá trị lớn nhất là 5 do đó đáp án B đúng.
Ngoài ra ta xác định được các tiệm cận ngang như sau, khi x tiến đến \( + \infty \) thì y tiến đến 1, x tiến đến \( - \infty \) thì y tiến đến -2 do đó đồ thị có hai tiệm cận ngang là \(y = 1\) và \(y = - 2\). Do đó C đúng. Điểm cực tiểu của đồ thị là \(\left( {1;0} \right)\) do đó D đúng.
Suy ra còn lại đáp án A là sai do hàm số không có giá trị nhỏ nhất.
Vậy ta chọn A.
