Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 600. Hãy tính thể tích của khối chóp đó.. Bài 1.10 trang 20 sách bài tập (SBT) – Hình học 12 - Bài 3. Khái niệm về thể tích khối đa diện
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 600. Hãy tính thể tích của khối chóp đó.
Hướng dẫn làm bài:
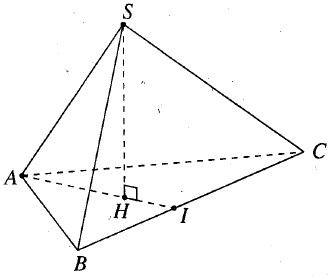
Kẻ \(SH \bot (ABC)\) . Đường thẳng AH cắt BC tại I.
Advertisements (Quảng cáo)
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của \(\Delta ABC\) .
Do đó \(AI = {{\sqrt 3 } \over 2}a,AH = {2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a,\widehat {SAH} = {60^0}\)
\(SH = AH.\tan {60^0} = {{\sqrt 3 } \over 3}a.\sqrt 3 = a\)
Thể tích khối chóp S.ABC là: \(V = {1 \over 3}.{1 \over 2}.{{\sqrt 3 } \over 2}a.a.a = {{\sqrt 3 } \over {12}}{a^3}\)