Bài 1.17 trang 21 sách bài tập (SBT) – Hình học 12: Cho hình hộp ABCD.A’B’C’D’. Gọi E và F lần lượt là trung điểm của...

Cho hình hộp ABCD.A’B’C’D’ . Gọi E và F lần lượt là trung điểm của B’C’ và C’D’ . Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và (H’), trong đó (H) là hình đa diện chứa đỉnh A’. Tính tỉ số giữa thể tích hình đa diện (H) và thể tích hình đa diện (H’).

Hướng dẫn làm bài:

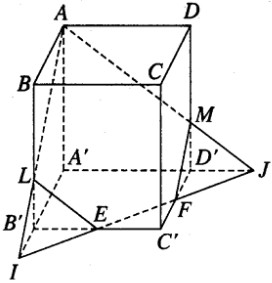
Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M. Gọi V₀ là thể tích khối tứ diện AA’IJ.  V là thể tích khối hộp ABCD.A’B’C’D’

Vì EB’ = EC’ và B’I // C’F  nên $IB’ = FC’ = {{A’B’} \over 2}$

Do đó  ${{IB’} \over {IA’}} = {1 \over 3}$

Để ý rằng  BE’ // A’J  , B’L //AA’

Ta có  ${{IL} \over {IA}} = {{IE} \over {{\rm{IJ}}}} = {{IB’} \over {IA’}} = {1 \over 3}$

Từ đó suy ra:  ${{{V_{I.ELB’}}} \over {{V_{I.JAA’}}}} = {({1 \over 3})^3} = {1 \over {27}}$

Do đó  ${V_{I.ELB’}} = {1 \over {27}}{V_0}$

Tương tự  ${V_{J.MFD’}} = {1 \over {27}}{V_0}$

Gọi AB = a, BC = b , đường cao hạ từ A xuống (A’B’C’D’) là h thì

$V = {V_{ABCD.A’B’C’D’}} = hab.\sin \widehat {BAD}$,

${V_0} = {1 \over 3}({1 \over 2}.{{3a} \over 2}.{{3b} \over 2}\sin \widehat {BAD})h = {{3V} \over 8}$

Vậy  ${V_{(H)}} = {V_0} - {2 \over {27}}{V_0} = {{25} \over {27}}{V_0} = {{25} \over {27}}.{{3V} \over 8} = {{25} \over {72}}V,{V_{(H’)}} = {{47} \over {72}}V$,

${V_{(H’)}} = {{47} \over {72}}V,{{{V_{(H)}}} \over {{V_{(H’)}}}} = {{25} \over {47}}$