Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 600.Hãy tính thể tích của khối chóp đó.
Hướng dẫn làm bài:
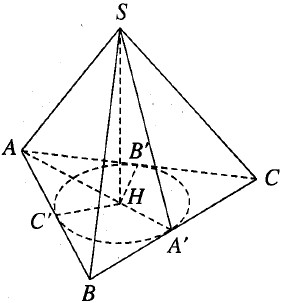
Kẻ \(SH \bot (ABC)\) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có \(SA’ \bot BC,SB’ \bot CA,SC’ \bot AB\)
Từ đó suy ra \(\widehat {SA’H} = \widehat {SB’H} = \widehat {SC’H} = {60^0}\).
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó, AA’2 = AB2 – BA’2 = 25a2 – 9a2 = 16a2
Advertisements (Quảng cáo)
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó \({S_{ABC}} = {1 \over 2}6a.4a = 12{a^2} = pr = 8ar\)
Từ đó suy ra \(r = {3 \over 2}a\)
Do đó \(SH = HA’.\tan {60^0} = {{3a} \over 2}\sqrt 3 = {{3\sqrt 3 } \over 2}a\)
Thể tích khối chóp là \(V = {1 \over 3}.12{a^2}.{{3\sqrt 3 } \over 2}a = 6\sqrt 3 {a^3}\).
