Cho hình lăng trị ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a và tạo với đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a.
Hướng dẫn làm bài:
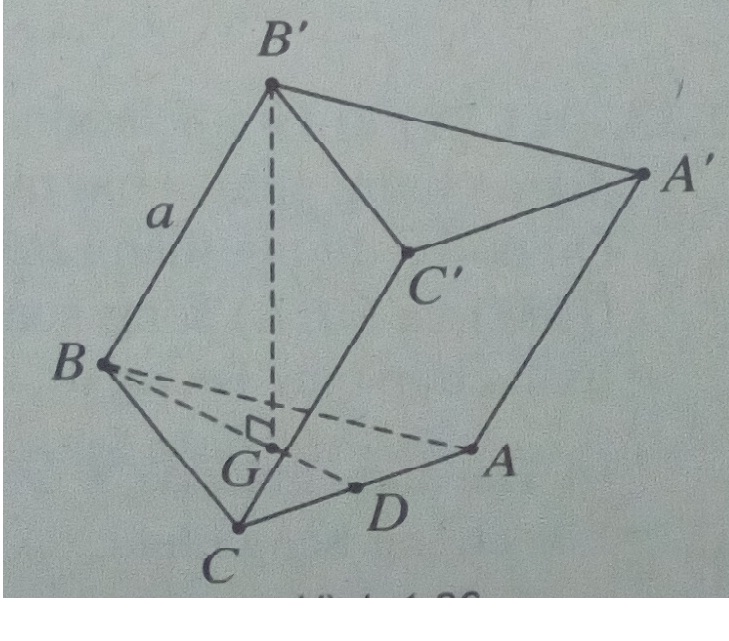
Gọi G là trọng tâm của tam giác ABC, khi đó \(\widehat {B’BG} = {60^0},B’G = {{a\sqrt 3 } \over 2},BG = {a \over 2}\)
Gọi D là trung điểm của AC, khi đó \(BD = {{3a} \over 4}\) .
Advertisements (Quảng cáo)
Ta có BC2 + CD2 = BD2 , do đó \(B{C^2} + {{B{C^2}} \over 4} = {{5B{C^2}} \over 4} = {{9{a^2}} \over {16}}\)
Suy ra \(B{C^2} = {9 \over {20}}{a^2},{S_{ABC}} = {{B{C^2}} \over 2} = {9 \over {40}}{a^2}\)
\({V_{ABC.A’B’C’}} = {{a\sqrt 3 } \over 2}.{{9{a^2}} \over {40}} = {{9\sqrt 3 } \over {80}}{a^3}\)
