Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:
\({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}} = {1 \over r}\)
Hướng dẫn làm bài:
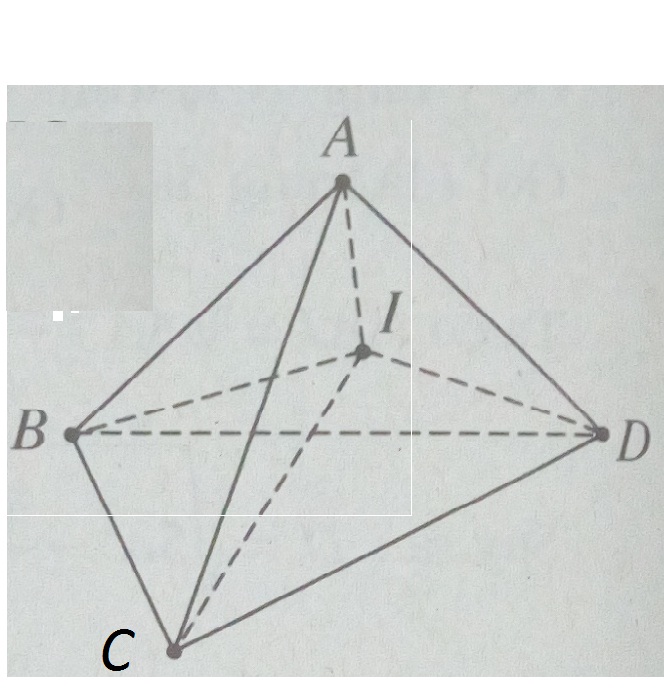
Gọi I là tâm mặt cầu nội tiếp tứ diện, V là thể tích tứ diện. Ta có
Advertisements (Quảng cáo)
\(V = {V_{IBCD}} + {V_{ICDA}} + {V_{IDAB}} + {V_{IABC}}\)
\( \Rightarrow I = {{{V_{IBCD}}} \over V} + {{{V_{ICDA}}} \over V} + {{{V_{IDAB}}} \over V} + {{{V_{IABC}}} \over V}\)
\(= {{{1 \over 3}r{S_{BCD}}} \over {{1 \over 3}{h_A}{S_{BCD}}}} + {{{1 \over 3}r{S_{CDA}}} \over {{1 \over 3}{h_B}{S_{CDA}}}} + {{{1 \over 3}r{S_{DAB}}} \over {{1 \over 3}{h_C}{S_{DAB}}}} + {{{1 \over 3}r{S_{ABC}}} \over {{1 \over 3}{h_D}{S_{ABC}}}}\)
\( = r({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}})\)
\(\Rightarrow {1 \over r} = {1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}\)
