Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.. Bài 1.34 trang 22 sách bài tập (SBT) – Hình học 12 - ĐỀ TOÁN TỔNG HỢP - CHƯƠNG I. KHỐI ĐA ĐIẾN
Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.
Hướng dẫn làm bài:
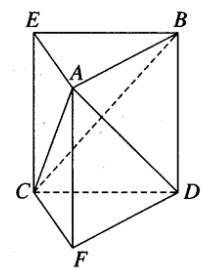
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Advertisements (Quảng cáo)
Ta có: \({S_{ABE}} = {1 \over 2}ab.\sin {60^0} = ab{{\sqrt 3 } \over 4}\) ,
\({V_{C.ABE}} = {1 \over 3}.{{\sqrt 3 } \over 4}ab.h = {{\sqrt 3 } \over {12}}abh\)
Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = {{\sqrt 3 } \over {12}}abh\)
