Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 600, AB = 2a , BC = a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a.
Hướng dẫn làm bài:
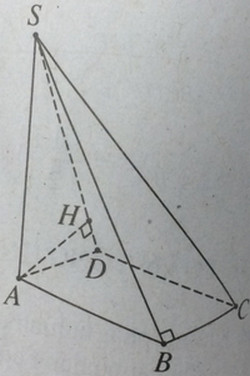
Vì các mặt (SAB) và (SAD) vuông góc với đáy nên \(SA \bot (ABCD)\) . Ta có:
\(\left\{ {\matrix{{BC \bot AB} \cr {BC \bot SA} \cr} } \right. \Rightarrow BC \bot (SAB)\)
⟹ góc\(((SBC),(ABCD)) = \widehat {SBA} = {60^0}\)
Advertisements (Quảng cáo)
Do đó: \(SA = 2a\tan {60^0} = 2a\sqrt 3 \)
\({V_{S.ABCD}} = {1 \over 3}2a\sqrt 3 .2a.a = {{4\sqrt 3 } \over 3}{a^3}\)
Vì CD // AB nên d(AB. CD) = d(AB, (SCD)). Hạ \(AH \bot SD\) , để ý rằng \(CD \bot (SAD) \Rightarrow AH \bot (SCD)\).
Do đó d(AB, SC) = AH.
Ta có: \(AH.SD = SA.AD\)
\(\Rightarrow AH = {{SA.AD} \over {\sqrt {S{A^2} + A{D^2}} }} = {{2a\sqrt 3 .a} \over {\sqrt {12{a^2} + {a^2}} }} = 2\sqrt {{3 \over {13}}} a\)
