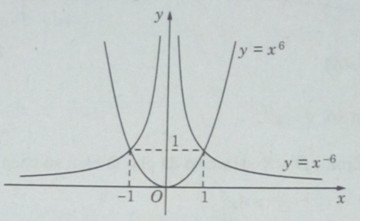
Vẽ đồ thị của hai hàm số sau trên cùng một hệ trục tọa độ:
\(y = {x^6}\) và \(y = {x^{ - 6}}\)
Hướng dẫn làm bài:
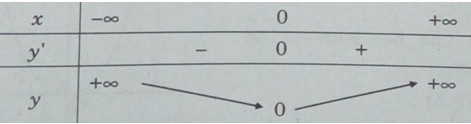
* Xét hàm số y = x6
Tập xác định D = R. Hàm số đã cho là hàm số chẵn.
\(\eqalign{
& y’ = 6{x^5} \cr
& \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to + \infty } = + \infty \cr} \)
Đồ thị không có tiệm cận
Bảng biến thiên
Advertisements (Quảng cáo)
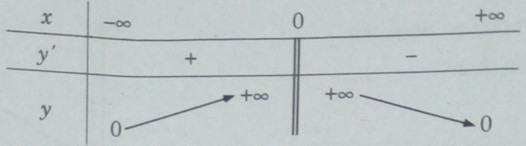
* Xét hàm số \(y = {x^{ - 6}}\)
Tập xác định: D = R\{0}. Hàm số đã cho là hàm số chẵn.
\(\eqalign{
& y’ = - 6{x^{ - 7}} \cr
& \mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr} \)
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
Đồ thị của các hàm số \(y = {x^6},y = {x^{ - 6}}\) như sau. Các đồ thị này đều có trục đối xứng là trục tung.