Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện:
a) |z – i| = 1
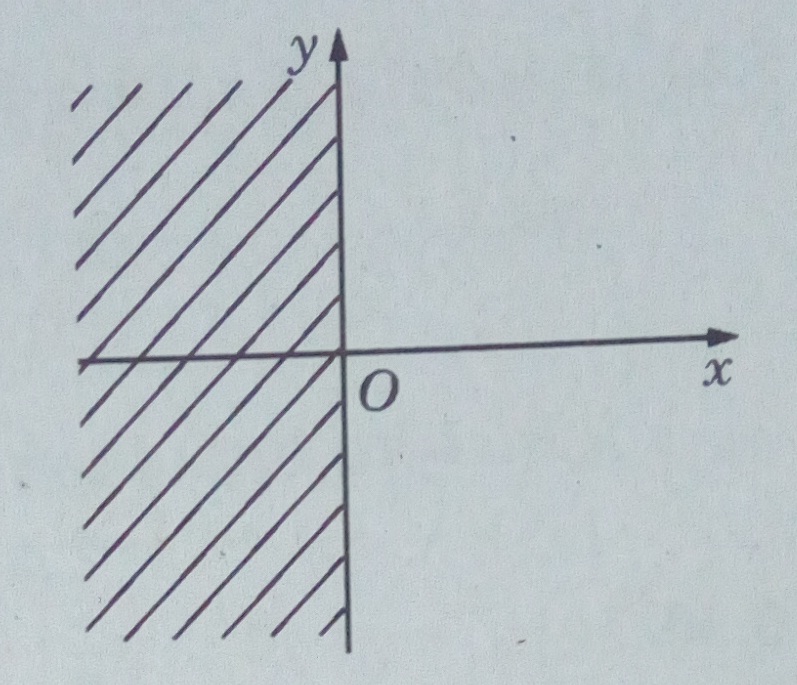
b) |2 + z| < |2 – z|
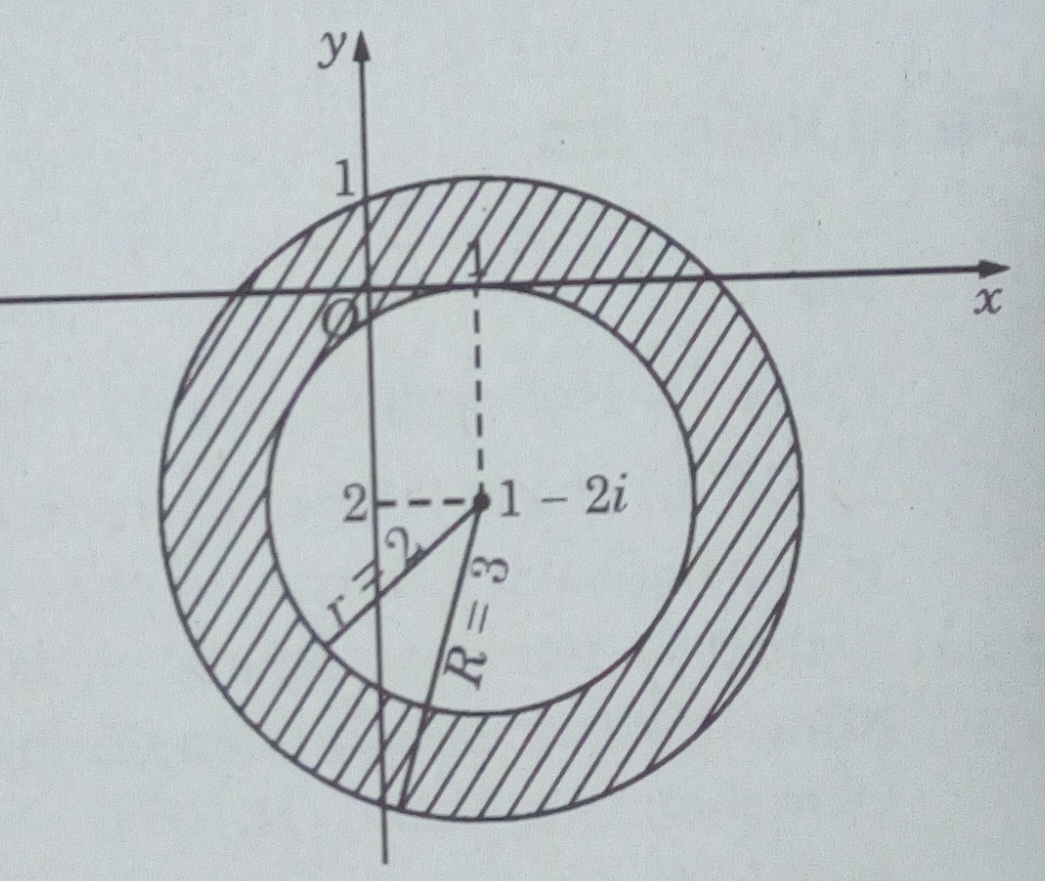
c) \(2 \le |z - 1 + 2i| < 3\)
Hướng dẫn làm bài:
a) Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1)
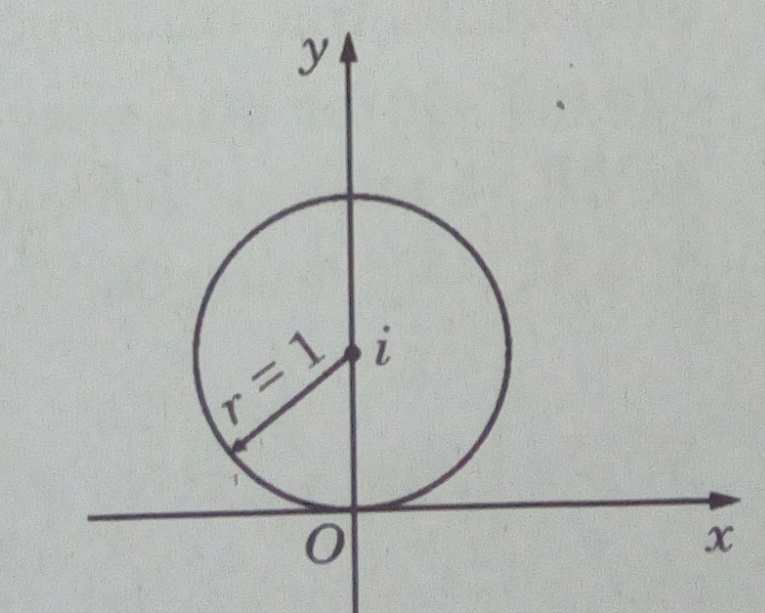
Ta có thể tiến hành như sau:
Cho \(z = x + iy\) , ta có \(|z - i{|^2} = |x + (y - 1)i{|^2} = {x^2} + {(y - 1)^2}\) và như vậy ta có: \({x^2} + {(y - 1)^2} = 1\)
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
Advertisements (Quảng cáo)
b)
Ta có: \(|2 + z{|^2} < |2 - z{|^2}\)
\(\Leftrightarrow |(2 + x) + iy{|^2} < |(2 - x) - iy{|^2}\)
\(\Leftrightarrow {(2 + x)^2} + {y^2} < {(2 - x)^2} + {( - y)^2}\)
\(\Leftrightarrow x < 0\)
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.
c) Đó là những điểm nằm phía trong hình tròn bán kính bằng 3 và phía ngoài (kể cả biên) hình tròn bán kính bằng 2 có cùng tâm là điểm biểu diễn số phức z0 = 1 – 2i , tức là những điểm nằm trong hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện: \(4 \le {(x - 1)^2} + {(y + 2)^2} < 9\)