Chứng minh các bất đẳng thức sau:
a) \({e^x} + \cos x \ge 2 + x - {{{x^2}} \over 2},\forall x \in R\)
b) \({e^x} - {e^{ - x}} \ge 2\ln (x + \sqrt {1 + {x^2}} ),\forall x \ge 0\)
c) \(8{\sin ^2}{x \over 2} + \sin 2x > 2x,\forall x \in (0;\pi {\rm{]}}\)
Hướng dẫn làm bài
a) Xét hàm số \(f(x) = {e^x} + \cos x - 2 - x + {{{x^2}} \over 2}\) , có tập xác định là R.
\(f'(x) = {e^x} - \sin x - 1 + x;f'(x) = 0 \Leftrightarrow x = 0\)
Ta lại có \(f”(x) = {e^x} + 1 - \cos x > 0,\forall x\) vì \(1 - \cos x \ge 0\) và \({e^x} > 0\)
Như vậy, f’(x) đồng biến trên R. Từ đó: \(f'(x) < f'(0) = 0,\forall x < 0;f'(x) > f'(0) = 0,\forall x > 0\)
Ta có bảng biến thiên
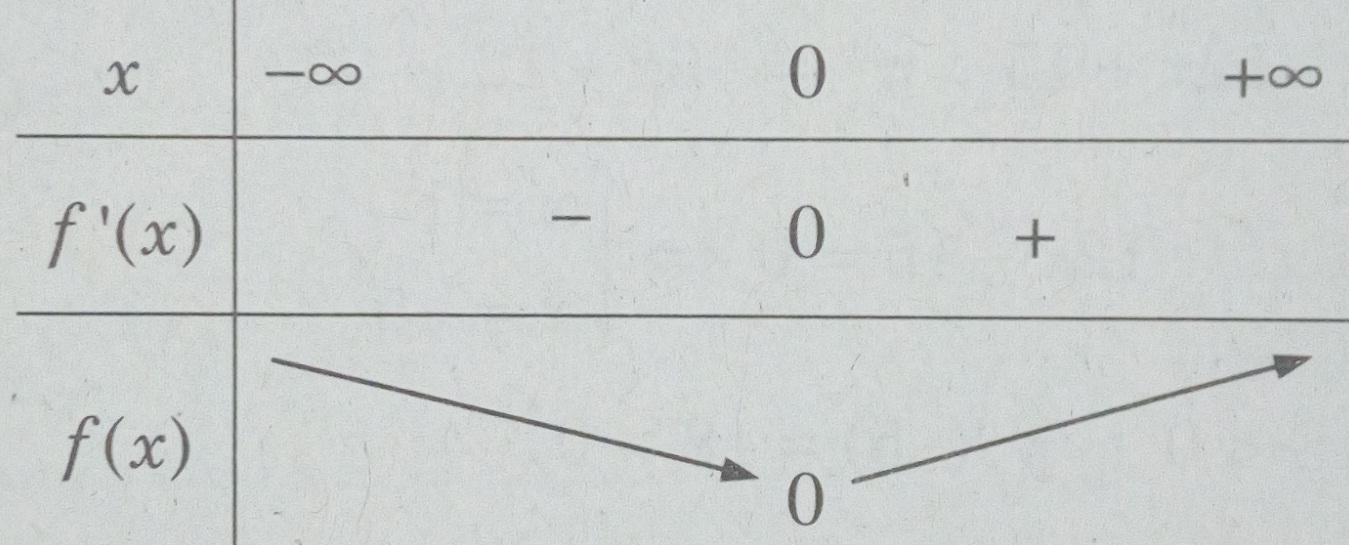
Hàm số \(f(x) = {e^x} + \cos x - 2 - x + {{{x^2}} \over 2} \ge {f_{CT}} = f(0) = 0,\forall x \in R\)
Từ đó suy ra điều phải chứng minh.
Advertisements (Quảng cáo)
b) \(\forall x \ge 0\) xét hàm số \(f(x) = {e^x} - {e^{ - x}} - 2\ln (x + \sqrt {1 + {x^2}} )\) , ta có
\(f'(x) = {e^x} + {e^{ - x}} - {2 \over {\sqrt {1 + {x^2}} }}\) ;
Từ đó f ‘(x) > 0 với mọi x > 0 (vì \({e^x} + {e^{ - x}} > 2\) và \({2 \over {\sqrt {1 + {x^2}} }} < 2\) ) và \(f ‘(x) = 0 \Leftrightarrow x = 0\)
Vậy f(x) đồng biến trên \({\rm{[}}0; + \infty )\) , tức là:
\(f(x) \ge f(0) = {e^0} - {e^0} - 2\ln 1 = 0\)
Từ đó suy ra điều cần chứng minh
c) Xét hàm số \(f(x) = 8{\sin ^2}{x \over 2} + \sin 2x - 2x,\forall x \in (0;\pi {\rm{]}}\)
\(f'(x) = 4\sin x + 2\cos 2x - 2 = 4\sin x(1 - \sin x)\)
\(f'(x) = 0 \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2}} \cr {x = \pi } \cr} } \right.\)
Với \(x \in (0;\pi {\rm{]}}\) ta có \(f'(x) \ge 0\) và dấu bằng chỉ xảy ra tại hai điểm.
Vậy f(x) đồng biến trên nửa \((0;\pi {\rm{]}}\). Mặt khác, f(0) = 0 nên f(x) > 0.
Từ đó suy ra điều phải chứng minh.
