Câu hỏi/bài tập:
Cho hàm số \(y = f\left( x \right) = x + 1\). Với mỗi \(x \ge 1\), kí hiệu \(S\left( x \right)\) là diện tích của hình thang giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng vuông góc với \(Ox\) tại các điểm có hoành độ 1 và \(x\).
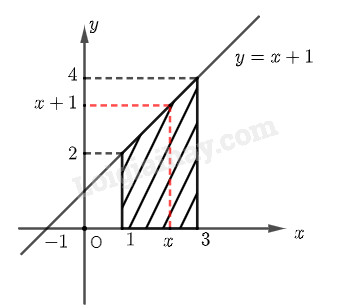
a) Tính \(S\left( 3 \right)\).
b) Tính \(S\left( x \right)\) với mỗi \(x \ge 1\).
c) Tính \(S’\left( x \right)\). Từ đó suy ra \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\left[ {1; + \infty } \right)\).
d) Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Chứng tỏ rằng \(F\left( 3 \right) - F\left( 1 \right) = S\left( 3 \right)\). Từ đó nhận xét về cách tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\).

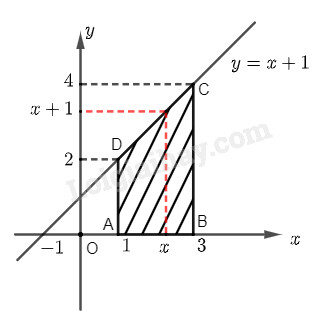
a, b) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Tính độ dài các cạnh \(AD\), \(BC\) và \(AB\), rồi sử dụng công thức tính diện tích hình thang \({S_{ABCD}} = \frac{{\left( {AD + BC} \right).AB}}{2}\) để tính \(S\left( 3 \right)\) ở câu a và \(S\left( x \right)\) ở câu b.
c) Sử dụng công thức đạo hàm để tính \(S’\left( x \right)\) và kết luận.
d) Tính nguyên hàm của \(f\left( x \right)\), sau đó tính \(F\left( 3 \right) - F\left( 1 \right)\), so sánh với \(S\left( 3 \right)\)

Advertisements (Quảng cáo)
a) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Dễ thấy rằng \(ABCD\) là hình thang vuông có hai đáy là \(AD\) và \(BC\), chiều cao là \(AB\).
Ta có \(AB = 3 - 1 = 2\), \(AD = 2\) và \(BC = 4\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( 3 \right) = \frac{{\left( {2 + 4} \right).2}}{2} = 6\).
b) Tương tự câu a, nhưng hoành độ của \(B\) là \(x\), ta suy ra tung độ của \(C\) là \(x + 1\).
Ta có \(AB = x - 1\), \(AD = 2\), \(BC = x + 1\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( x \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + x + 1} \right)\left( {x - 1} \right)}}{2} = \frac{{\left( {x + 3} \right)\left( {x - 1} \right)}}{2} = \frac{{{x^2} + 2x - 3}}{2}\)
c) Ta có \(S’\left( x \right) = \frac{{2x + 2}}{2} = x + 1 = f\left( x \right)\). Vậy \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\).
d) Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\), ta có:
\(F\left( x \right) = \int {f\left( x \right)dx} = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C\)
Suy ra \(F\left( 3 \right) = \frac{{{3^2}}}{2} + 3 + C = \frac{{15}}{2} + C\) và \(F\left( 1 \right) = \frac{{{1^2}}}{2} + 1 + C = \frac{3}{2} + C\)
Như vậy ta có \(F\left( 3 \right) - F\left( 1 \right) = \left( {\frac{{15}}{2} + C} \right) - \left( {\frac{3}{2} + C} \right) = 6 = S\left( 3 \right)\).
Do đó, để tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\), ta thực hiện tính nguyên hàm \(F\left( x \right)\) của \(f\left( x \right)\), sau đó ta tính \(F\left( 3 \right)\) và \(F\left( 1 \right)\), từ đó tính được \(S\left( 3 \right) = F\left( 3 \right) - F\left( 1 \right)\).
