Câu hỏi/bài tập:

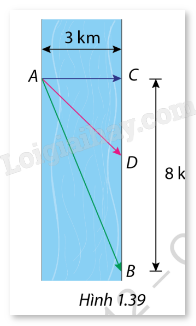
Một người chèo thuyền từ điểm A trên bờ một con sông thẳng, rộng 3 km và muốn đến điểm B, cách bờ đối diện 8 km về phía hạ lưu, càng nhanh càng tốt như Hình 1.39. Người ấy có thể chèo thuyền qua sông đến điểm C rồi chạy bộ đến B, hoặc anh ta có thể chèo thuyền đến D nào đó giữa C và B rồi chạy bộ đến B. Tốc độ chèo thuyền là 6 km/h và tốc độ chạy bộ là 8 km/h. Tìm thời gian ngắn nhất mà người này có thể đi từ A đến B (bỏ qua vận tốc của nước và làm tròn kết quả đến hàng phần trăm).

- Đặt biến ? là khoảng cách từ điểm C đến điểm D.
- Thiết lập hàm số ?(?) thời gian tổng quát bao gồm thời gian chèo thuyền và thời gian chạy bộ.
- Khảo sát hàm số ?(?).
- Tính thời gian tại giá trị ? tìm được để đảm bảo đó là thời gian ngắn nhất.

- Gọi ? là khoảng cách từ điểm C đến điểm D (BC≥?≥0).
Advertisements (Quảng cáo)
- Quãng đường từ A đến D là: \(\sqrt {{3^2} + {x^2}} = \sqrt {9 + {x^2}} \)km.
- Thời gian chèo thuyền là: \(\frac{{\sqrt {9 + {x^2}} }}{6}\) giờ.
- Thời gian chạy bộ từ D đến B là:\(\frac{{8 - x}}{8}\) giờ.
→ Tổng thời gian: \[T(x) = \frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\]
- Khảo sát hàm số ?(?):
Tính đạo hàm: \({T^\prime }(x) = \frac{1}{6} \cdot \frac{x}{{\sqrt {9 + {x^2}} }} - \frac{1}{8}\)
Giải phương trình \({T^\prime }(x) = 0\) :
\(\begin{array}{l}\frac{x}{{6\sqrt {9 + {x^2}} }} = \frac{1}{8}\\ \Rightarrow 8x = 6\sqrt {9 + {x^2}} \\ \Leftrightarrow 64{x^2} = 36\left( {9 + {x^2}} \right)\\ \Leftrightarrow 64{x^2} = 324 + 36{x^2}\\ \Leftrightarrow 28{x^2} = 324\\ \Rightarrow x = \sqrt {\frac{{324}}{{28}}} = \frac{{924}}{{\sqrt 7 }} \approx 3.4\end{array}\)
Bảng biến thiên:

Thời gian ngắn nhất mà người này có thể đi từ A đến B là 1.33 giờ.
