Mục 2 trang 44 Toán 12 tập 1 - Cùng khám phá: Cho hàm số y = f(x) = x^3 - 3x^2 + 3 Sử dụng phần mềm GeoGebra vẽ đồ thị...

Cho hàm số $y = f(x) = {x^3} - 3{x^2} + 3$

a) Sử dụng phần mềm GeoGebra vẽ đồ thị (C) của hàm số đã cho.

b) Tìm nghiệm gần đúng (làm tròn đến hàng phần trăm) của phương trình $f(x) = 0$

c) Dựa vào đồ thị đã vẽ ở câu a, biện luận theo tham số m số nghiệm của phương trình ${x^3} - 3{x^2} + 3 = m$.

a) Mở GeoGebra và nhập hàm số f(x).

b) Sử dụng câu lệnh Nghiem( Đa thức ) để tìm các nghiệm gần đúng.

c)

- Tạo thanh trượt m và vẽ hàm số y = m

- Quan sát và biện luận

a)

- Mở GeoGebra và nhập hàm số $f(x) = {x^3} - 3{x^2} + 3$

- Đồ thị của hàm số sẽ trông như sau:

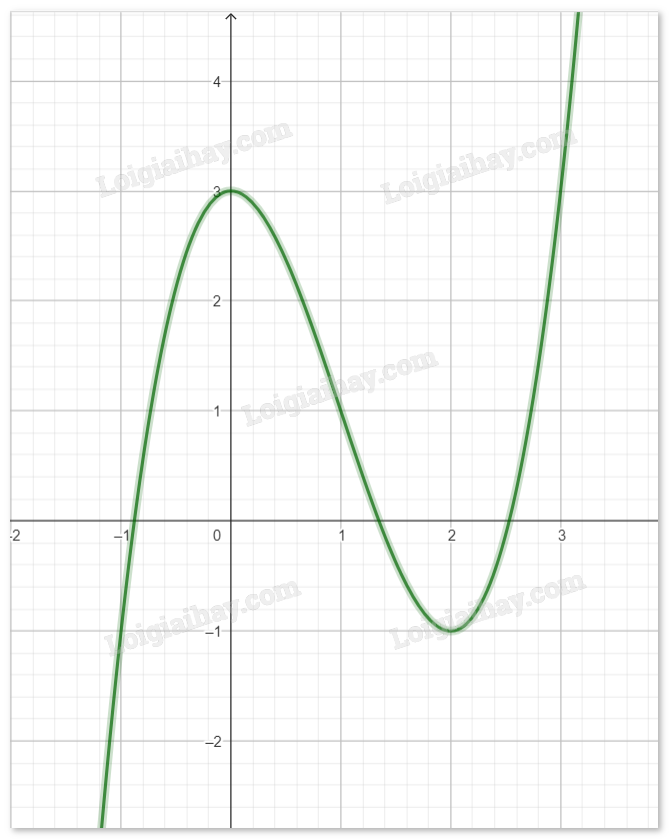
b) Sử dụng câu lệnh Nghiem(Đa thức) để tìm các điểm mà đồ thị cắt trục x sẽ ra được kết quả như sau:

Từ đó, ta thấy phương trình $f(x) = 0$ có các nghiệm là: ${x_1} \approx - 0.88,{x_2} \approx 1.35,{x_3} \approx 2.53$

c)

- Tạo thanh trượt m với m nằm trong khoảng (-5,5)

- Vẽ đồ thị hàm số y = m

- Số giao điểm của hai đồ thị sẽ là nghiệm của phương trình ${x^3} - 3{x^2} + 3 = m$(*)

- Kéo thanh trượt m ta sẽ thấy sự thay đổi của các nghiệm

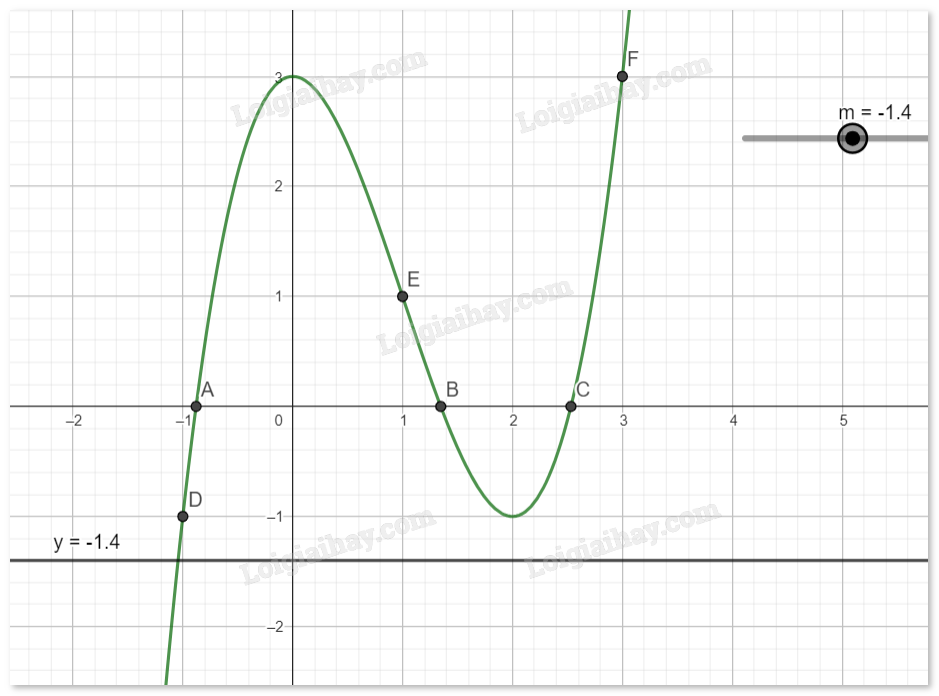
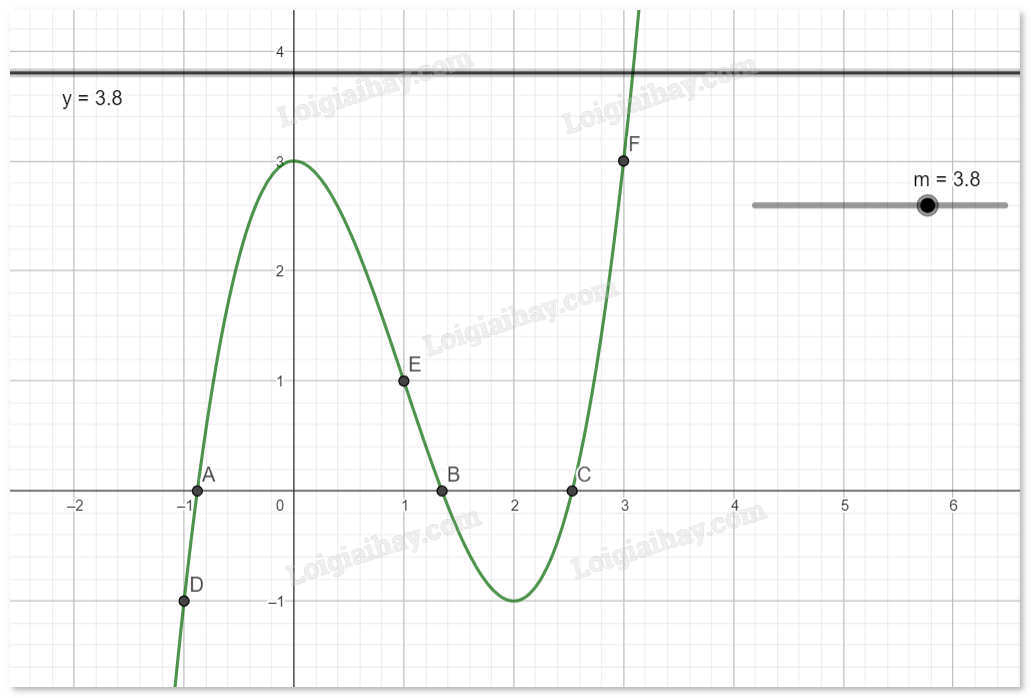
Với $m > 3$, phương trình (*) có 1 nghiệm.

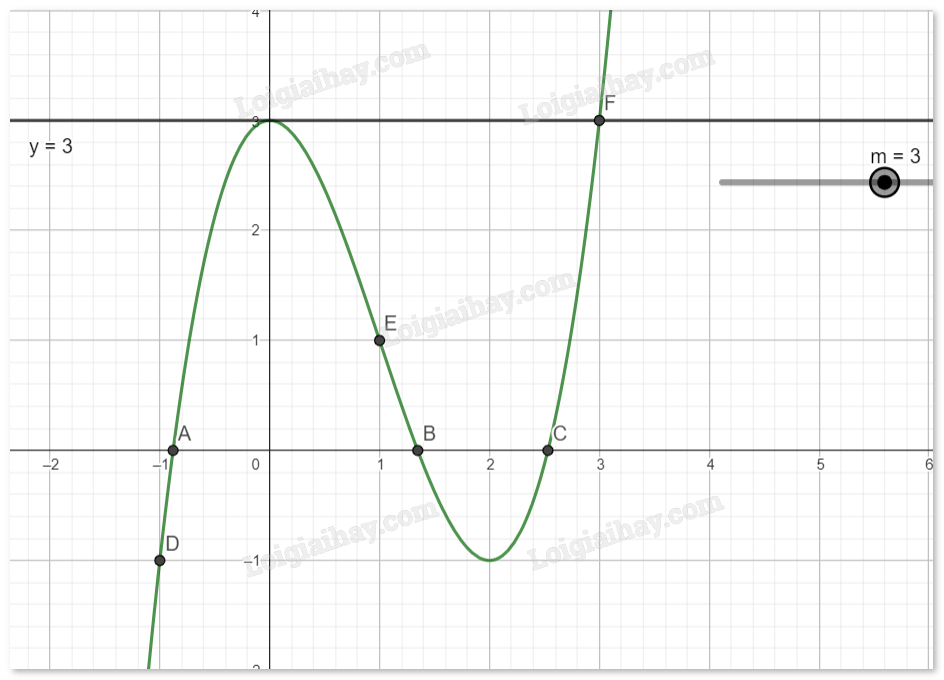
Với $m = 3$, phương trình (*) có 2 nghiệm.

Với \( - 1

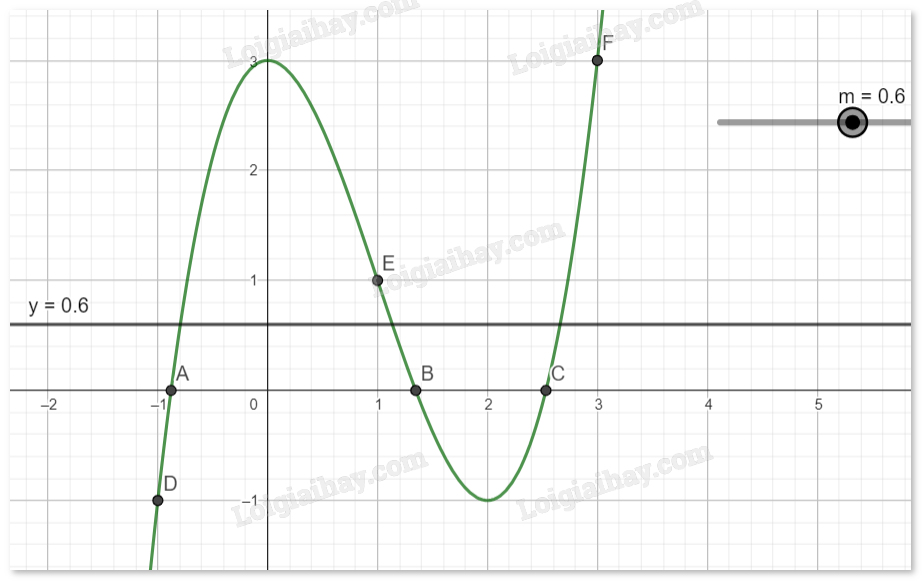
Với $m = - 1$, phương trình (*) có 2 nghiệm.

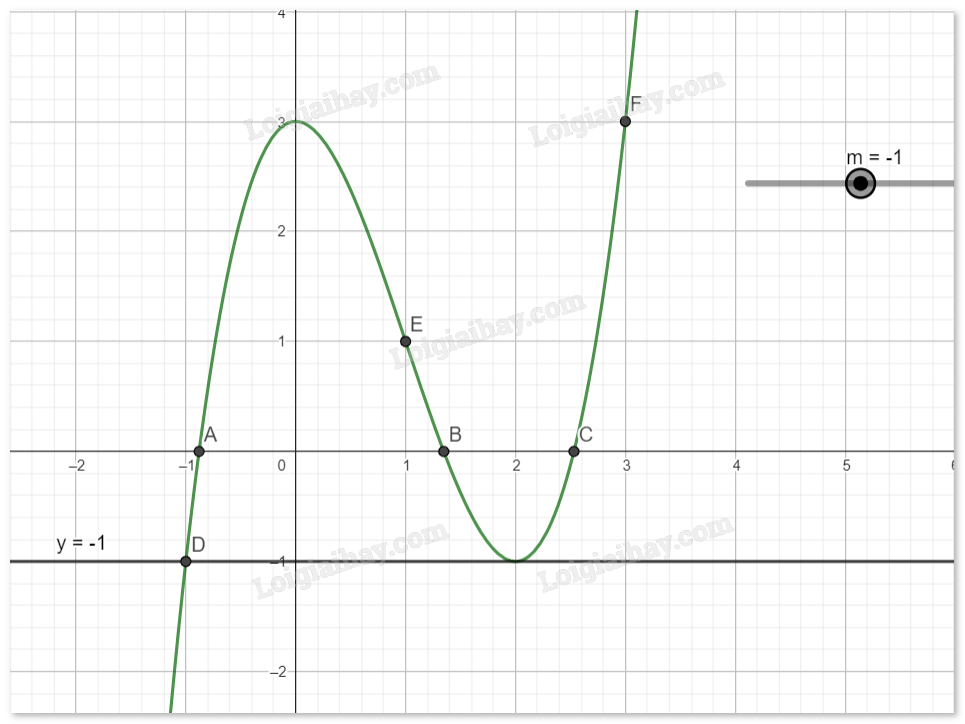
Với \(m